102- Uma força de 100 N, que faz um ângulo θ para cima com um piso horizontal, é aplicada a uma cadeira de 25,0 kg em repouso no piso. Se θ = 0°, determine (a) a componente horizontal da força aplicada e (b) o módulo da força normal exercida pelo piso sobre a cadeira. Se θ = 30,0°, determine (c) e (d) . Se θ = 60,0°, determine (e) e (f) . Suponha que o coeficiente de atrito estático entre a cadeira e o piso é 0,420. A cadeira escorrega ou permanece em repouso se θ é (g) 0°, (h) 30,0° e (i) 60,0°?
Passo 1
Tratando a cadeira como um bloco temos o seguinte sistema de forças.
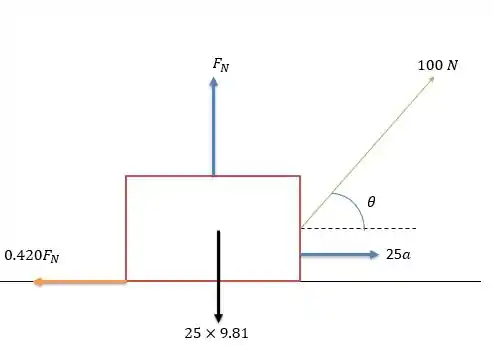
Já que nesse caso é um piso horizontal.
Fazendo a somatória das forças verticais, adotando positivo como o norte, temos:
Onde temos que espelhar a força de na vertical.
Isolando :
Fazendo a resultante das forças horizontais temos:
Passo 2
Vamos aos enunciados. As letras a e b pedem e quando , então:
a)
b)
As letras c e d a mesma coisa mas pra .
c)
d)
Finalmente as letras e e f pedem a mesma coisa só que para .
e)
f)
Passo 3
Agora a condição para saber se há escorregamento ou não basta saber se:
Onde o coeficiente de atrito vale
g)
Para :
Como não é maior que , logo a cadeira não se locomove (ou não escorrega, ou está em repouso).
h) Para
Como a afirmação é verdadeira então pode se dizer que a cadeira movimenta.
i)Para :
Como a afirmação é falsa, logo para esse ângulo a cadeira está em repouso.