Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 5.Problemas - Ex. 55
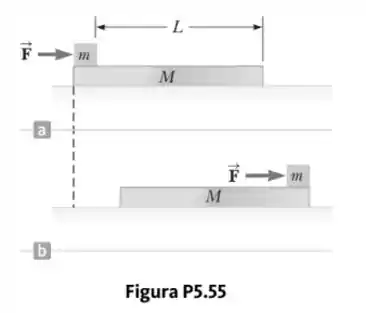
Um bloco de massa repousa na extremidade esquerda de outro de massa . O coeficiente do atrito cinético entre os dois blocos é e a superfície em que o bloco de repousa é sem atrito. Uma força horizontal constante de módulo é aplicada ao bloco de , colocando-o em movimento, como mostrado na Figura P5.55a. Se a distância que a extremidade dianteira do bloco menor percorre sobre o maior é ,
- em qual intervalo de tempo o bloco menor chegará ao lado direito do de , como mostrado na Figura P5.55b? (Observação: Ambos os blocos são colocados em movimento quando é aplicada.)
- Qual é a distância que o bloco de percorre no processo?
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer uma questãozinha aqui?
Vem comigo e bora!
Letra a:
Primeiro, desenhe um diagrama de corpo livre do bloco de cima:
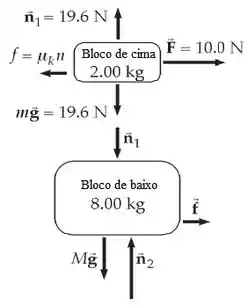
Uma vez que e
De temos:
Para o bloco de cima. Agora desenhe um diagrama de corpo livre do bloco de baixo (imagem a cima) e observe que nos dá:
Para o bloco de baixo.
No tempo t, a distância que cada bloco se move (começando do repouso) é:
Para o bloco de cima alcançar a borda direita do bloco de baixo, é necessário que :
Passo 2
Letra b:
De cima temos,