Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 75
Um bloco de aço de está em repouso sobre uma mesa horizontal. O coeficiente de atrito estático entre o bloco e a mesa é . (a) Qual é o módulo da força horizontal que coloca o bloco na iminência de se mover? (b) Qual é o módulo de uma força que, atuando a acima da horizontal, coloca o bloco na iminência de se mover? (c) Se a força atua a abaixo da horizontal, qual o valor máximo do seu módulo para que o bloco não se mova?
Passo 1
(a) Quando o bloco está na iminência de se mover, a força horizontal aplicada ao bloco e a força de atrito estático são iguais:
Como a mesa é horizontal, a força normal deve ser igual ao peso do objeto, então:
Passo 2
(b) Se a força atua acima da horizontal. A situação fica um pouco mais complicada:
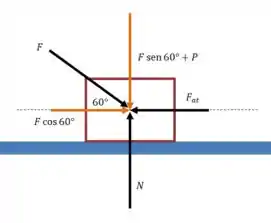
A lógica continua a mesma de antes: a força de atrito estático tem que ser igual à força horizontal.
Mas dessa vez a normal não é igual ao peso, como podemos ver pelo desenho:
Agora vamos substituir os valores numéricos:
Passo 3
(c) No caso em que a força age abaixo da horizontal, a componente horizontal da força continua a mesma, mas a componente vertical muda de sentido.
Agora a força está empurrando o bloco um pouco para cima, e então esta diminuindo o contato com o chão, e então diminuindo a força normal.
Então agora vamos pegar a equação que tínhamos antes:
E trocar o sinal de :
Resposta
(a) .
(b) .
(c) .