Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 16.Exercícios e Problemas - Ex. 14

Calcule o campo elétrico no ponto P da Figura 16.8, (a) aplicando diretamente a lei de Coulomb e (b) utilizando a fórmula para o campo de um dipolo elétrico.

Passo 1

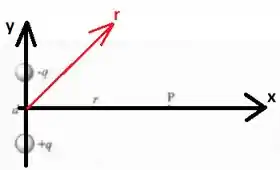
Primeiro vamos fazer um esboço da situação com os campos produzidos pelas cargas no ponto P :

Note que podemos escrever:

E → 1 = E   cos ⁡ θ   x ^ + s e n   θ   y ^

E → 2 = E   - cos ⁡ θ   x ^ + s e n   θ   y ^

Nessas expressões, E é o campo de uma carga pontual:

E = 1 4 π ϵ 0 ⋅ q r 2 + d 2 2

Com isso, somando os campos, vemos que

E → = 2 E   s e n   θ   y ^ = 1 2 π ϵ 0 ⋅ q r 2 + d 2 4   s e n   θ

Passo 2

Mas observe que

s e n   θ = d / 2 r 2 + d 2 4

Assim,

E → = 1 4 π ϵ 0 ⋅ q d r 2 + d 2 4 3 / 2   y ^

Passo 3

Agora vamos achar esse campo usando a fórmula do campo do dipolo. O potencial é dado por

φ r → = 1 4 π ϵ 0   p → ⋅ r ^ r 2 = 1 4 π ϵ 0   p → ⋅ r → r 3

O vetor p → aponta da carga negativa para a positiva:

p → = - q d   y ^

Seja θ o ângulo que r ^ faz com o eixo y :

Com isso, o produto p → ⋅ r → fica

p → ⋅ r → = - q d   r cos ⁡ θ

Podemos escrever y = r cos ⁡ θ , de modo que

φ x ,   y = - q d 4 π ϵ 0 ⋅ y x 2 + y 2 3 / 2

Note que esqueci completamente a componentes z pois o problema ocorre no plano x y .

Passo 4

Para achar o campo elétrico nós usamos a relação

E → = - ∇ φ

Assim,

E x = - ∂ φ ∂ x               e           E y = - ∂ φ ∂ y

Portanto,

E x = + q d 4 π ϵ 0 ⋅ - 3 2 ⋅ y x 2 + y 2 5 2 ⋅ 2 x

E y = + q d 4 π ϵ 0 x 2 + y 2 3 2 - y ⋅ 3 2 x 2 + y 2 1 2 ⋅ 2 y x 2 + y 2 3

No ponto P , temos x = r e y = 0 , de modo que

E x = 0           e         E y = q d 4 π ϵ 0 ⋅ 1 r 3

Portanto,

E → = 1 4 π ϵ 0 ⋅ q d r 3   y ^

Observe que para d muito pequeno as expressões são praticamente idênticas!

Resposta

E → = 1 4 π ϵ 0 ⋅ q d r 2 + d 2 4 3 / 2   y ^

E → = 1 4 π ϵ 0 ⋅ q d r 3   y ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Por que é possível blindar uma sala contra forças elétricas, mas não contra forças gravitacionais?
Suponha que a superfície da Terra tivesse uma carga líquida que não fosse zero. Porque seria ainda possível adotar a Terra como ponto referencial padrão de potencial e atribuir-lhe o potencial V = 0 ?
Por que o elétron-volt é frequentemente uma unidade mais conveniente para energia do que o joule?
Como poderíamos comparar um próton-volt a um elétron-volt? A massa de um próton é 1.840 vezes a massa de um elétron.
Em um relâmpago típico, a diferença de potencial entre e a terra é de 1,0 × 10 9V e a quantidade de carga transferida é de 30C . (a) Qual é a variação de energia da carga transferida? (b) Se toda a en