Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 17.Exercícios e Problemas - Ex. 17
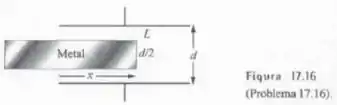
Calcule a variação da força sobre o bloco metálico da Figura 17.16 com a coordenada , sabendo-se que o capacitor está ligado a uma bateria que mantém uma voltagem fixa entre as placas.
Passo 1
No exercício 15 nós achamos que a capacitância desse sistema é dada, em função de , por
Aqui temos que tomar um cuidado, como agora quem está fixo é ddp (e não a carga), temos que usar a relação
Assim,
Passo 2
Derivando a capacitância nós achamos
Portanto,
Ou ainda,
Note que agora a força é negativa, de modo que o metal é repelido do capacitor!
Resposta
Exercícios de Livros Relacionados
Um capacitor cilíndrico possui um condutor interno com raio de 1,5 mm e um condutor externo com raio de 3,5 mm. Os dois condutores estão separados pelo vácuo e o comprimento total do capacitor é de 2,
Na figura 24.26, seja C 1 = 6,0 μ F , C 2 = 3,0 μ F e C 3 = 5,0 μ F . O circuito de capacitores está conectado a um potencial aplicado V a b . Quando as cargas dos capacitores atingem os seus valores
Na figura abaixo, seja C 1 = 3,0μ F , C 2 = 5,0μ F e V a b = + 52,0 V . Calcule (a) a carga em cada capacitor e (b) a diferença de potencial através de cada capacitor.
Na figura abaixo, cada capacitor possui C =4μ F e V a b = + 28V .Calcule (a) a carga de cada capacitor; (b) a diferença de potencial através de cada capacitor; (c) a diferença de potencial entre os po
Uma esfera condutora maciça, de raio R , possui uma carga Q . Calcule a densidade de energia do campo elétrico em um ponto situado a uma distância r do centro da esfera para (a) rR ; (b) rR . (c) Calc