Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 16.Exercícios e Problemas - Ex. 20
Um dipolo elétrico está à distância de uma carga , alinhado na orientação radial, como mostra a Figura 16.11. Calcule a força exercida sobre o dipolo.
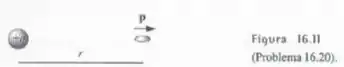
Passo 1
Para resolver esse problema, temos que primeiro achar o campo elétrico produzido pela carga na posição do dipolo. Para isso, vamos adotar um sistema de coordenadas:
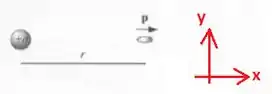
O campo produzido pela carga na posição do dipolo será o campo de uma carga pontual:
Passo 2
Como apresentado na seção 16.7 pela equação 16.54, a força sobre o dipolo vai depender da variação do campo com a distância:
Com isso,
Portanto,
Resposta
Exercícios de Livros Relacionados
47 . Uma carga puntiforme q 1 = 4,00n C é colocada na origem, e uma segunda carga puntiforme q 2 = - 3,00n C é colocada sobre o eixo x no ponto x = + 20,0c m . Uma terceira carga puntiforme q 3 = 2,00
50 . Uma pequena esfera com massa igual a 5,00 × 10 - 7k g e carga igual a + 7,00μ C é liberada a partir do repouso a uma distância de 0,400m acima de uma grande placa isolante horizontal uniformement
52 . Um próton e uma partícula alfa são liberados a partir do repouso quando estão separados por 0,225n m de distância. A partícula alfa (um núcleo de hélio) tem, essencialmente, quatro vezes a massa
51 . Determinação do tamanho do núcleo. Quando o rádio- 226 decai radioativamente, ele emite uma partícula alfa (o núcleo de hélio), e o produto final é o radônio- 222 . Podemos modelar essa decadênci
46 . Uma carga puntiforme q 1 = + 5,00μ C está fixa no espaço. A partir de uma distância horizontal de 6,00c m , uma pequena esfera com massa igual a 4,00 × 10 - 3k g e carga q 2 = + 2,00μ C é lançada