Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 8.Problemas - Ex. 11

  1. Calcule (pela lei de Ampère ou Biot e Savart) o campo magnético B → devido a uma corrente I num fio retilíneo infinito, num ponto P à distancia R do fio. Demonstre, pela lei de Biot e Savart, que a porção do fio à esquerda de P contribui com B → ⋅ 1 2 .

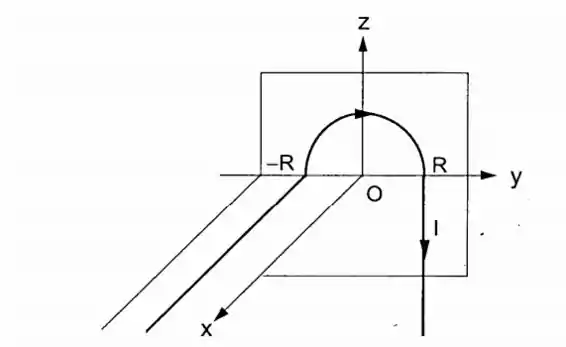
  2. Uma corrente continua de intensidade I percorre o fio representado na fig., que tem uma porção retilínea muito longa paralela a O z . Calcule o campo magnético B → produzido por esta corrente no ponto O , centro de semicírculo.

Passo 1

Para resolvermos, vamos considerar o fio infinito. Dessa forma, como já mostrado antes no capítulo, podemos calcular qual o campo gerado por uma corrente que passa pelo fio. Como já foi demonstrado passo a passo no livro como calcular para um fio, vamos apenas analisar a parte da contribuição a esquerda.

Passo 2

  1. Temos que pela integração do campo para o fio retilíneo infinito, chegamos no resultado de

    2. B = μ 0 i 2 π R φ →

    Mas e se não formos de + ∞ até - ∞ na hora da integração? Temos que aparece a seguinte integral antes de chegarmos nesse resultado:

    B = - 2 ∫ π 2 0 sin ⁡ θ R d θ ⋅ μ 0 i 4 π

    Esse termo 2 que aparece no inicio da nossa integral se deve ao fato de estarmos percorrendo desde - ∞ até + ∞ . Se pegarmos o valor apenas de - ∞ até 0 , teremos que nossa integral continuará com o mesmo intervalo de integração, porém sem esse termo 2 no inicio da integral, já que só queremos uma parte do fio, chegando então no valor de

    B 1 = μ 0 i 4 π R φ → = 1 2 ⋅ B →

    Passo 3

  2. Bom, aplicando Biot e Savart, podemos dividir todo esse fio em três partes, da seguinte forma:

B = ∫ d B r e t a + ∫ d B c u r v a + ∫ d B r e t a

Onde cada um representa um fio. Bom, das duas partes retas nós já sabemos pelo item anterior: como se trata de fios que vão de - ∞ até 0 e de 0 até - ∞ , temos que seu valor de campo será metade do valor total e aplicando a regra da mão direita, vemos que o campo na primeira integral apontará para z → , na segunda integral será para x → e na terceira o mesmo. Assim, ficamos com nosso campo como

B = μ 0 I 4 π R z → + ∫ d B c u r v a + μ 0 I 4 π R x →

Vamos calcular então da parte curva. Temos que, como d l → será perpendicular com a direção de r → , nosso φ = 90 º . Assim, temos que d l → × r → = d l → . Temos que sua integral então será

B c u r v a = μ 0 I 4 π R 2 ⋅ ∫ d l → = μ 0 I 4 π R 2 ⋅ θ R

Onde θ R é o arco (caminho) percorrido pela corrente. Como temos um semicírculo, nosso θ será no valor de π . Assim, nossa segunda integral fica

B c u r v a = μ 0 I 4 R

E o resultado final ficará

B = μ 0 I 4 π R ⋅ π + 1 x → + z →

Resposta

  1. B → = μ 0 i 2 π R φ →
  2. B → = μ 0 I 4 π R ⋅ π + 1 x → + z →
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

44- Um solenóide toroidal (veja Exemplo 28.10 ) possui raio interno r 1 = 15.0c m e raio externo r 2 = 18.0c m . O solenóide possui 250 espiras e conduz uma corrente de 8.50A . Qual é o módulo do camp
45- Um anel de madeira com diâmetro médio igual a 14.0c m é enrolado de modo compacto com 600 espiras, formando um enrolamento toroidal. Determine o campo magnético em um ponto situado no centro da se
43- Um campo magnético de 37.2T foi obtido no Francis Bitter National Magnetic Laboratory, do M I T . Determine a corrente necessária para atingir esse campo. ( a ) a 2.0c m de um fio longo e retilíne
64- O fio retilíneo longo A B , indicado na Figura 28.57 , conduz uma corrente de 14.0A . A espira retangular cuja aresta mais longa é paralela ao fio conduz uma corrente de 5.0A . Determine o módulo,
69- O fio na Figura 68.61 conduz uma corrente I no sentido indicado. O fio é constituído por uma seção retilínea longa, uma seção correspondente a um quarto de circunferência e outra seção retilínea l