Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 5.Problemas - Ex. 4
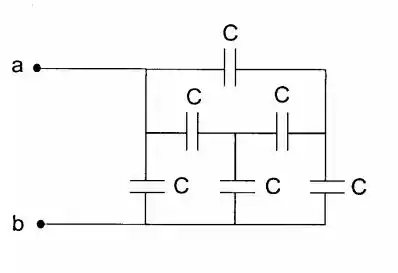
Mostre que é possível substituir o sistema de capacitores da figura por um único capacitor equivalente netre os ponstos e e calcule a capacitância deste capacitor.
Passo 1
Para resolvermos, vamos usar o conceito de capacitância equivalente para substituir toda essa quantidade de capacitores por um apenas, analisando sempre como estão conectados e os caminhos que a tensão segue.
Passo 2
Bom, vamos analisar através da tensão que passa por cada capacitor, esse método que, na minha opinião, se torna mais simples. Primeiro vamos nomear cada capacitor da seguinte forma:
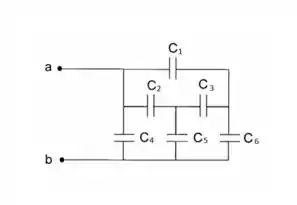
Se observarmos bem o primeiro nó, a carga total do circuito será a soma de :
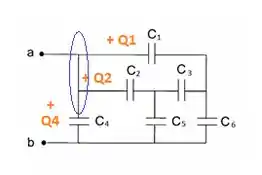
Assim, temos que nossa carga total é
Lembrando que a capacitância é dada por:
onde é a diferença de potencial entre e .
Passo 3
Vamos somar todas as tensões que passam cada capacitor, descobrir quanto valem e depois aplicar nessa equação acima. Temos que as tensões são dadas por:
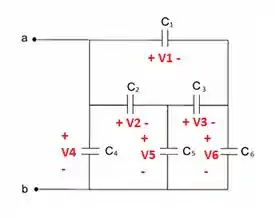
Olhando os capacitores 1 e 6:
Logo:
Olhando os capacitores 2, 3 e 6:
Logo:
Olhando os capacitores 2 e 5:
Logo:
Olhando o capacitor 4:
Logo:
Passo 4
Vamos olhar para as cargas dos capacitores que se encontram. A união entre os capacitores 2, 3 e 5:
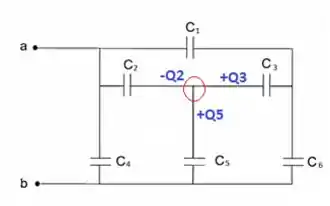
Logo a soma das cargas deve ser igual a zero:
Vamos colocar em função da tensão, não vamos esquecer que todos os capacitores tem o valor :
Dividindo tudo por e multiplicando por (-1):
A união entre os capacitores 2, 3 e 5:
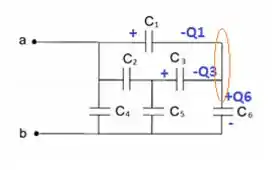
Logo a soma das cargas deve ser igual a zero:
Vamos colocar em função da tensão, não vamos esquecer que todos os capacitores tem o valor :
Dividindo tudo por :
Passo 5
Essas são todas as equações que precisamos. Logo de cara já conseguimos que , só precisamos agora de e . Vamos manipular primeiro a equação (1), escrevendo ela como
Agora manipulando nossa equação (6), teremos que
Substituindo em (7), teremos que
Se manipularmos agora nossa equação (5), teremos que
E (prometo que ta acabando gente, vamo la) manipulando agora a equação (3), vamos chegar que
Substituindo (10) em (11), vamos chegar que:
Igualando e , vamos chegar que , pois assim é o único jeito da equação ser satisfeita. Agora que temos , vamos achar e . Usando a (9), temos que
E como , podemos substituir em (11) para achar , que será
.
Substituindo agora na nossa equação para a capacitância equivalente, temos que
Como todos os capacitores tem capacitância , temos que nosso capacitor equivalente será de:
.