Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 119
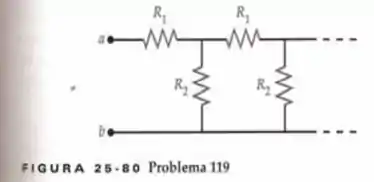
a) Calcule a resistência equivalente (em termos de R, a resistência de cada um dos resistores) entre os pontos a e b para a escada infinita de resistores mostrada na Figura 25-80, considerando que os resistores sejam idênticos. Isto é, considerando que .
b) Repita a parte (a), mas não considere que , e expresse sua resposta em termos de .
c) Confira seus resultados mostrando que o resultado para a parte (b) concorda com o da parte (a) se você substituir por e .
Passo 1
a)
Meus queridos e minhas queridas!
Sabemos que:
Resolvendo em função de :
Passo 2
b)
A letra b possui solução parecida com a da letra a.
Resolvendo em função de e considerando apenas o valor positivo:
Passo 3
c)
Para checar as relações, vamos substituir por :
Resposta
Exercícios de Livros Relacionados
Você recebeu uma bateria desconhecida. Usando seu multímetro você observa que, quando um resistor de 5Ω é conectado aos terminais da bateria, a corrente é de 0.5A . Quando este resistor é substituído
(a)Determine a resistencia equivalente entre os pontos a e b na figura 25.57. (b)Se a queda de potencial entre os pontos a e b é 12V , determine a corrente em cada resistor.
As baterias do circuito na figura 25-60 têm resistência interna desprezível. (a) Encontre a corrente usando a regra do loop de Kirchhoff. (b) Encontre a energia entregue ou fornecida por cada bateria.
Verifique seus resultados para o Problema 79 usando os seguintes valores específicos: (a) R1 = 4,00 Ω, R2 = 6,00 Ω; (b) R1 = 4,00 Ω, R3 = 3,00 Ω; e (c) R2 = 6,00 Ω, R3 = 3,00 Ω.
Na Figura 25-59, o emf da bateria é 6,00 V e R é 0,500 Ω. A taxa de aquecimento Joule em R é 8,00 W. (a) Qual é a corrente no circuito? (b) Qual é a diferença em potencial entre R? (c) Qual é a resist