Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.4 - Ex. 33

a) Calcule o torque desenvolvido por um motor industrial com potência de 150 kW para uma velocidade angular de 4000 rev/min. b) Um tambor de massa desprezível, com diâmetro

igual a 0,400 m, é ligado ao eixo do motor e a potência disponível do motor é usada para elevar um peso pendurado em uma corda enrolada em torno do tambor. Qual é o peso

máximo que pode ser elevado com velocidade constante? c) Com que velocidade constante o peso sobe?

Passo 1

Eaee, belezinha?? Bom... queremos calcular o torque τ desenvolvido por um motor industrial com potência P de 150   k W para uma velocidade angular ω de 4000   r e v / m i n .

Para isso, precisamos saber da seguinte expressão:

τ = P ω

Também o enunciado nos diz que um tambor de massa desprezível, com diâmetro igual a 0,400   m , é ligado ao eixo do motor e a potência disponível do motor é usada para elevar um peso pendurado em uma corda enrolada em torno do tambor.

Com isso, devemos calcular o peso máximo que pode ser elevado com velocidade constante.

Nesse caso, precisaremos fazer um diagrama de corpo livre para resolver essa questão.

Por fim, devemos calcular a velocidade constante com que o peso sobe.

E aí?? Bora lá!! 😉

Passo 2

  1. Nós vamos utilizar a equação P = τ ω e resolve-la para τ .

    2. ω deve ser dado em r a d / s , então:

    ω = 4000 r e v m i n ⋅ 2 π r a d 1 r e v ⋅ 1 m i n 60 s = 418,9 r a d / s

    Então,

    τ = P ω = 1,50 × 10 5 w a t t s 418,9 r a d / s = 358 N ⋅ m

    Passo 3

  2. Nós vamos aplicar a segunda lei de Newton ao tambor. E encontrar a tensão T na corda utilizando τ que calculamos no item a).

    3. Vamos desenhar o sistema em um diagrama de corpo livre:

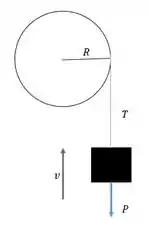
    Velocidade constante implica que a aceleração é nula, e T = P .

    τ = T R

    Isso implica que:

    T = τ R = 358 N ⋅ m 0,200 m = 1790 N

    Assim, um peso P = 1790 N pode ser levantado.

    Passo 4

  3. Aqui, vamos usar:

v = R ω

Sabemos que o ω = 418,9 r a d / s

Então,

v = 0,200 m ⋅ 418,9 r a d / s = 83,8 m / s

Resposta

  1. τ = 358 N ⋅ m
  2. T = 1790 N
  3. v = 83,8 m / s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O corpo da figura abaixo, pode girar em torno de um eixo perpendicular ao papel passando por O e está submetido a duas forças, como mostra a figura. Se r1=1,30 m, r2=2,15 m, F1=4,20 N, F2=4,90 N, θ 1
O comprimento do braço do pedal de uma bicicleta é 0,152 m e uma força de 111 N é aplicada ao pedal pelo ciclista. Qual é o módulo do torque em relação ao eixo do braço do pedal quando o braço faz um
O comprimento do braço do pedal de uma bicicleta é 0,152 m e uma força de 111 N é aplicada ao pedal pelo ciclista. Qual é o módulo do torque em relação ao eixo do braço do pedal quando o braço faz um
O comprimento do braço do pedal de uma bicicleta é 0,152 m e uma força de 111 N é aplicada ao pedal pelo ciclista. Qual é o módulo do torque em relação ao eixo do braço do pedal quando o braço faz um
Uma pequena bola de massa 0,75 Kg está presa a uma das extremidades de uma barra de 1,25 m de compimento e massa desprezível. A outra extremidade da barra está pendurada em um eixo. Qual é o módulo do