Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 67
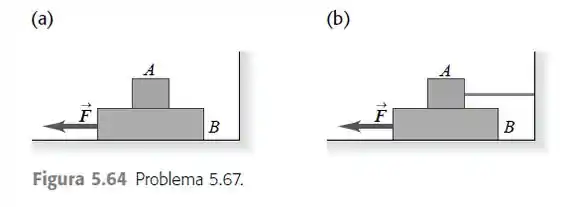
O bloco da Figura 5.64 pesa e o bloco pesa . O coeficiente de atrito cinético entre todas as superfícies é . Determine o módulo da força horizontal necessária para arrastar o bloco para a esquerda com velocidade constante, quando a) o bloco está sobre o bloco e se move com ele (Figura 5.64a); b) o bloco é mantido em repouso (Figura 5.64b).
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá o seguinte sistema:
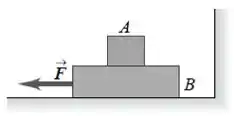
Queremos determinar o módulo da força horizontal necessária para arrastar o bloco para a esquerda com velocidade constante dado que:
- O bloco pesa ;
- o bloco B pesa ;
- O coeficiente de atrito cinético entre todas as superfícies é .
Depois temos que fazer a mesma coisa, mas considerando o bloco mantido em repouso.
Para resolver essa questão, nós vamos aplicar a segunda lei de Newton para cada bloco:
Depois vamos usar a terceira lei de Newton (ação e reação) para relacionarmos o bloco e o bloco .
Lembrando que velocidade constante significa que a aceleração é nula.
Agora vamos analisar cada situação !!
Passo 2
- Nesta situação, como os blocos se movem juntos, podemos tratá-los como um objeto só. Logo, a força peso será:
- Agora já não podemos mais tratar os blocos com um objeto só.
Vamos desenhar também o diagrama de corpo livre para essa combinação:
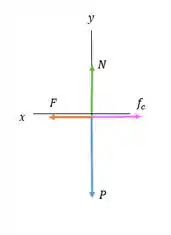
E então vamos aplicar a segunda lei de Newton sobre ele:
No :
E
No :
Passo 3
Então vamos desenhar o diagrama de corpo livre para cada bloco em separado:
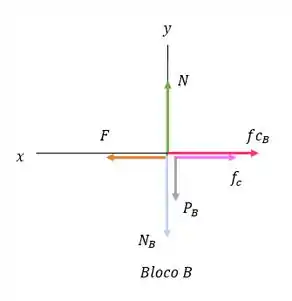
e são os normais e as forças de atrito aplicadas ao bloco B pela mesa são as mesmas da parte (a).
é a força de atrito que A aplica-se a B. É à direita porque a força de A se opõe ao movimento de B.
é a força descendente que A exerce sobre B.
é a força de atrito que B aplica a A. Está à esquerda porque o bloco B quer que A se mova com ele.
A é a força normal que o bloco B exerce sobre A.
Passo 3
Pela terceira lei de Newton,
e essas forças estão em direções opostas.
Além disso,
e essas forças estão em direções opostas.
Passo 4
E então, vamos aplicar a segunda lei de Newton para os blocos separadamente:
Para o bloco A na vertical:
Então,
Temos que:
E
Passo 5
Para o bloco A na horizontal:
Passo 6
Para o bloco B na horiontal:
Na parte (a), o bloco A está em repouso em relação a B e tem aceleração zero.
Não há força horizontal em A além do atrito, e a força de atrito em A é zero. Uma força maior é necessária na parte (b), devido ao força de atrito entre os dois blocos.