Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 27.Problemas - Ex. 60
No canhão de elétrons de um cinescópio de TV, os elétrons (carga e massa m) são acelerados por uma voltagem V. Depois de abandonar o canhão de elétrons, o feixe de elétrons percorre uma distância D no sentido da tela; nessa região existe um campo magnético transversal de módulo B e não há nenhum campo elétrico. (a) Desenhe a trajetória do feixe de elétrons no tubo. (b) Mostre que o desvio aproximado do feixe produzido pelo campo magnético é dado por
(Sugestão: Posicione a origem no centro do arco do feixe de elétrons e compare uma trajetória do feixe sem desvio com outra com desvio).
Passo 1
letra a)
O feixe se desloca no sentido da tela e tem um desvio produzido pelo campo. Então temos:
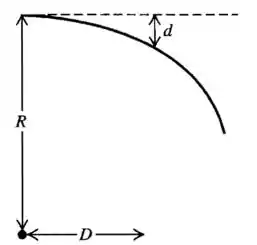
Passo 2
letra b)
Vamos considerar que esse elétron tem uma trajetória circular de raio .
Se a partícula não sofresse uma deflexão:
Já quando consideramos a deflexão, no eixo do a partícula se desloca , temos:
Então o desvio será:
Para
Passo 3
Para descobrirmos o raio da órbita, precisamos igualar a força centrípeta com a força magnética.
Então:
Como não tem o termo da velocidade na expressão que devemos encontrar, precisamos achar uma expressão para a velocidade.
Passo 4
Como a partícula é acelerada a partir de uma diferença de potencial, podemos usar CONSERVAÇÃO DE ENERGIA!
O desvio será então:
Passo 5
Calculando agora o desvio com os dados do enunciado:
Como equivale a mais de de , então ele é uma valor significante.
Resposta
letra a)
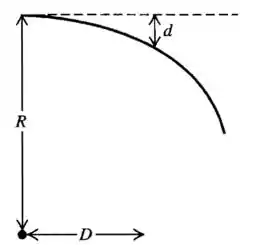
letra c). é significante.