Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 28.Problemas Adicionais - Ex. 88
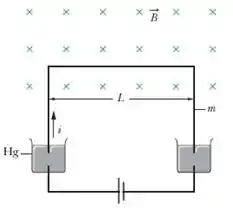
Na Fig. 28-57, as duas extremidades de um fio em forma de U, de massa e comprimento, estão imersas em mercúrio (que é um condutor), formando uma espira. Um campo magnético uniforme de módulo é aplicado perpendicularmente ao plano da espira. Uma chave (que não aparece na figura) é fechada e aberta rapidamente, criando um pulso de corrente que se propaga na espira e faz o fio se deslocar para cima. Se altura máxima atingida pelo fio em relação à posição inicial é , qual é a carga do pulso? Suponha que a duração do pulso é muito menor que o tempo de subida do fio. (Sugestão: Use a definição de impulso, Eq. 9-30, a relação entre impulso e momento, Eq. 9-31, e a relação entre carga e corrente, Eq. 26-2.)
Passo 1
Usando a definição de impulso e igualando com a variação do momento linear temos:
A força aqui é a força magnética e como ela faz um ângulo de com o campo magnético e com a velocidade a expressão para essa força é :
E sabendo da relação de carga e corrente, a carga contida num pulso de duração é :
Então a carga desse pulso é:
Passo 2
O fio inicialmente em respouso é submetido a um impulso que o lança verticalmente para cima com uma velocidade , atingindo uma altura máxima de . Na altura máxima a velocidade dele é nula. Bom, da cinemática sabemos que a velocidade inicial de um corpo que atinge a altura máxima é:
Passo 3
Assim, juntando a expressão para a carga com a velocidade temos:
Os dados que o problema nos trás são:
Daí é só substituir: