Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 37.Exercícios e Problemas - Ex. 15
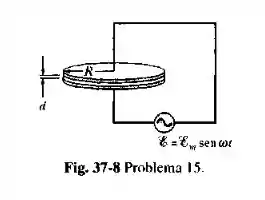
O capacitor na Fig. 37-8 consistindo em duas placas circulares de raio está ligado a uma fonte de f.e.m , onde e . O valor máximo da corrente de deslocamento é . Despreze a distorção do campo elétrico nas bordas das placas.
a. Qual é o valor máximo da corrente ?
b. Qual é o valor máximo de , onde é o fluxo elétrico na região entre as placas?
c. Qual a separação entre as placas?
d. Determine o valor máximo do módulo de entre as placas a uma distância do centro.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A - Suponha que temos um capacitor circular de placas paralelas, conectado a uma f,e.m , onde , e . O valor máximo da corrente de deslocamento é dado por . A corrente de condução nos fios é igual à corrente de deslocamento em qualquer instante, então a corrente máxima é:
Passo 2
B - A corrente de deslocamento é dada por:
A taxa do fluxo máximo é, portanto
Fazendo a substituição
Passo 3
C - A corrente de deslocamento é dada por:
Onde , então,
O campo elétrico entre as placas é igual a diferença de potencial através da placa dividida pela separação entre eles:
A diferença de potencial através do capacitor é igual à diferença de potencial da fonte, então:
A corrente máxima deslocada ocorre quando , então:
Isolando o , temos que
Substituindo os termos
Passo 4
D - A lei de Ampere-Maxwell em termos da corrente de deslocamento é dada por:
Dentro do círculo não há corrente regular fechada, então a lei se reduz a:
Em , a corrente fechada é igual à razão da área fechada com raio de sobre toda a área do campo elétrico com raio de , então:
O campo magnético é paralelo ao comprimento do elemento, e temos também que
Logo, temos que
O campo magnético máximo em ocorre quando , então:
Substituindo pelos dados para obter:
Portanto,