Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 29.Exercícios e Problemas - Ex. 76

Uma carga de 1,0 nC encontra-se na origem de um sistema de coordenadas. Uma carga de - 3 u C encontra-se sobre o eixo x em x = 4,0 c m . Encontre todos os pontos do plano xy nos quais o potencial é nulo. Expresse sua resposta na forma de um mapa de contorno, mostrando a linha equipotencial correspondente a V = 0 V .

Passo 1

Faaaala galera do Responde Aí

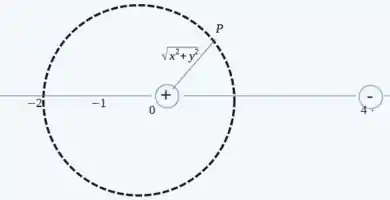
Olhando a figura, podemos dizer que o potencial elétrico no ponto P, é igual ao potencial gerado pela carga positiva mais o potencial gerado pela carga negativa

V = 1 4 π ε 0 1,0 ⋅ 10 - 9 x 2 + y 2 + 1 4 π ε 0 - 3,0 ⋅ 10 - 9 x 2 + y 2

Como queremos um potencial nulo

0 = 1 4 π ε 0 1,0 ⋅ 10 - 9 x 2 + y 2 + 1 4 π ε 0 - 3,0 ⋅ 10 - 9 4 - x 2 + y 2

Podemos multiplicar os dois lados por 4 π ε 0

0 = 1,0 ⋅ 10 - 9 x 2 + y 2 + - 3,0 ⋅ 10 - 9 4 - x 2 + y 2

Passo 2

Vamos passar um termo para o lado esquerdo.

3,0 ⋅ 10 - 9 4 - x 2 + y 2 = 1,0 ⋅ 10 - 9 x 2 + y 2

3,0 ⋅ 10 - 9 x 2 + y 2 = 1,0 ⋅ 10 - 9 4 - x 2 + y 2

Dividindo por 10 - 9

3,0 x 2 + y 2 = 4 - x 2 + y 2

Também vai ser interessante elevar ao quadrado os dois lados da equação

9 x 2 + 9 y 2 = 4 - x 2 + y 2

Passo 3

Podemos simplificar ainda mais

9 x 2 + 9 y 2 = 16 + x 2 - 8 x + y 2

8 x 2 + 8 x + 8 y 2 - 16 = 0

Perceba que

8 x 2 + 8 x = 8 x + 1 2 2 - 2

Colocando esse novo termo

8 x + 1 2 2 - 2 + 8 y 2 - 16 = 0

x + 1 2 2 + y 2 = 18 8

Eis a nossa reposta! A equação de uma circunferência. Esses são os pontos em que o potencial elétrico é nulo.

x + 1 2 2 + y 2 = 9 4

Resposta

x + 1 2 2 + y 2 = 9 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A FIGURA Q29.13 mostra três pontos nas proximidades de duas cargas puntiformes. As cargas possuem módulos iguais. Ordene em sequência, do mais positivo para o mais negativo, os potenciais de V a a V c
Reproduza a FIGURA Q29.14 sobre uma folha de papel. Depois desenhe um ponto (ou vários pontos) sobre a figura para indicar a posição (ou posições) em que o potencial elétrico é nulo.
Um dipolo elétrico possui momento de dipolo p. Para r ≫ s , onde s é a separação entre as cargas, mostre que o potencial elétrico do dipolo pode ser escrito como V = 1 4 π ε 0 ⋅ p c o s θ r 2 onde r é
O arranjo de cargas mostrado na FIGURA P29.68 é chamado de quadripolo elétrico linear. As cargas positivas estão localizadas em y = ± s . Note que a carga total do quadripolo é nula. Obtenha uma expre