Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 28
Uma carga puntiforme de e uma carga puntiforme de estão separadas por uma distância . Onde deveria ser colocada uma terceira carga puntiforme para que a força elétrica nesta terceira carga fosse igual a zero?
Passo 1
Veja o esquema a seguir:
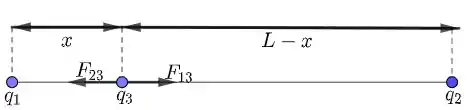
Note que a terceira carga deve ser colocada na reta que une as duas cargas. Isso ocorre, pois será o único modo das forças e terem a mesma direção, de modo que a força resultante poderá ser nula.
Além disso, na figura, supomos que . Porém, nada mudaria se .
Passo 2
Veja que
No equilíbrio,
Tirando a raiz quadrada, temos
Resposta
Devemos colocá-lo a da carga de .
Exercícios de Livros Relacionados
Na descarga de retorno de um relâmpago típico, uma corrente de 2,5 ×10 4A é mantida por 20μ s . Qual é o valor da carga transferida?
Uma partícula com uma carga de + 3,00 ×10 - 6C está a 12c m de distância de uma segunda partícula com uma carga de - 1,50 ×10 - 6C . Calcule o módulo da força eletrostática entre aspartículas.
Da carga Q que uma pequena esfera contém inicialmente, uma parte q é transferida para uma segunda esfera situada nas proximidades. As duas esferas podem ser consideradas cargas pontuais. Para que valo
Duas partículas de mesma carga são colocadas a 3,2 × 10 - 3 m de distância uma da outra e liberadas a partir do repouso. A aceleração inicial da primeira partícula é 7,0m / s 2 e a da segunda é 9,0m /
Qual deve ser a distância entre a carga pontual q 1=26,0μ C e a carga pontual q 2 = - 47,0μ C para que a força eletrostática entre as duas cargas tenha um módulo de 5,70N ?