Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 27
Três cargas puntiformes estão no eixo : está em , está na origem e está em . Determine a força elétrica em .
Passo 1
Temos o seguinte esquema:
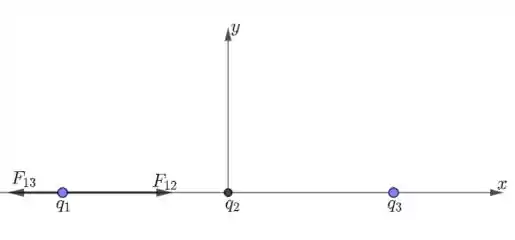
Note que a força entre e , é de atração. Seu valor é:
A força entre e é de repulsão. Seu valor é:
A força resultante será:
Note que tal força está orientada no sentido positivo do eixo . Assim,
Resposta
A força resultante é .
Exercícios de Livros Relacionados
Na Fig. 21-24, as cargas das partículas são q 1=- q 2=100n C e q 3=-q 4=200n C . O lado do quadrado é a=5,0c m . Determine (a) a componente x e (b) a componente y da força eletrostática a que está sub
Na Fig. 21-25, a partícula 1 , de carga + q , e a partícula 2 , de carga + 4,00 q , estão a uma distância L=9,00c m uma da outra em um eixo x . Se as três partículas permanecem onde estão quando uma p
Na Fig. 21-27 a, as partículas 1 e 2 têm uma carga de 20,0μ C cada uma e estão separadas por uma distância d=1,50m . (a) Qual é o módulo da força eletrostática que a partícula2 exerce sobre a partícul
Na Fig. 21-31, as partículas 1 e 2 , de carga q 1=q 2=+3,20 × 10 - 19C , estão no eixo y , a uma distância d=17,0c m da origem. A partícula 3 , de carga q 3=+ 6,40 ×10 - 19 C , é deslocada ao longo do
As cargas e coordenadas de duas partículas mantidas fixas no plano x y são q 1=+ 3,0μ C , x 1=3,5c m , y 1=0,50c m e q 2= - 4,0μ C , x 2=- 2,0c m , y 2=1,5c m . Determine (a) o módulo e (b) a orientaç