Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 21.4 - Ex. 5
Da carga que uma pequena esfera contém inicialmente, uma parte é transferida para uma segunda esfera situada nas proximidades. As duas esferas podem ser consideradas cargas pontuais. Para que valor de a força eletrostática entre as duas esferas é máxima?
Passo 1
E aí! tudo certinho? 😎
Nesse problema temos duas esferas, umas com carga e outra com carga neutra. Parte da carga da esfera carregada é passada para a esfera neutra e essa esera passa a ter carga .
A partir disso queremos saber qual é a ração de modo que a força eletrostática entre as esferas seja máxima.
Tem ideia de como fazemos isso? 🤔
Primeiro, pense no que acontece quando a partícula de carga doa uma carguinha para a outra esfera que antes era neutra, ou seja, não tinha carga nenhuma:
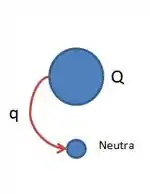
Nós vamos ficar com a esfera que doou com a seguinte carga:
Ou seja, vai ser a carga inicial menos a que ela doou para a outra esfera. E a segunda esfera? Ela tinha uma carga inicial nula (ela era neutra) e recebeu uma carga q, logo a carga dela será:
Então vamos ficar com o seguinte esquema:
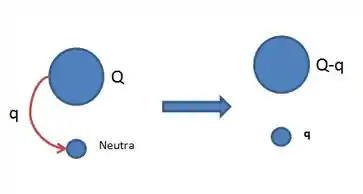
Após essa doação, a esfera menor da Figura fica eletrizada com carga e a esfera maior passa a ter uma carga menor do que a que ela tinha antes, igual a .
Tranquilo até aqui? 😁
Passo 2
Beleza! Já temos uma visão do problema, mas a questão pergunta pra gente sobre a força eletrostática. Vamos, então, usar a fórmula dessa força que é:
E quem são esses elementos da fórmula? São:
- é a força que desejamos calcular entre as cargas;
- é a constante eletrostática;
- é a carga da primeira esfera;
- é a carga da segunda esfera;
- é a distância entre as duas esferas carregadas.
Vamos então aplicar os nossos valores na fórmula? Bora!
Substituindo
E
Repare que essa força é máxima quando a expressão atinge seu valor máximo.
Sacou? 😊
Passo 3
Para a gente encontrar o valor de que corresponde a esse máximo, basta a gente derivar essa expressão e igualá-la a zero. Pois lá do cálculo, a gente tem que a devidada igual a zero nos dá o ponto de valor máximo ou mínimo (e nesse caso, ela vai nos dar o nosso valor máximo).
Fazendo isso, podemos achar o valor de que responde à pergunta:
Derivando , vamos derivar o outro lado em relação a :
Para encontrar o máximo, igualamos essa derivada a zero:
Logo:
Como queremos encontrar desde o enunciado a relação entre :
Acabou, meu amigo, chegamos na resposta final!
Entendeu tudo? Responde Aí! 😉
