Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 47
47. Um carrinho de montanha-russa de , parte do repouso de uma altura (Figura 7-46) acima da base de um loop de de diâmetro. Se o atrito é desprezível, determine a força para baixo exercida pelos trilhos sobre o o carrinho, quando ele está no topo do loop, de cabeça para baixo.
Passo 1
E aí, tudo bem? Bom, a primeira coisa para se resolver um problema como esse, que envolve energia e força, é definir a origem do nosso referencial de potencial gravitacional , que olhando bem a figura do enunciado, de cara sacamos que é conveniente que seja a base do loop. Vamos lá agora, tentar entender o que está se passando nessa questão!
O que acontece nesse exercício é que o carrinho sai do repouso de uma altura inicial , adquire velocidade e basicamente faz uma volta de 360° sobre o laço. Que tipos de energia então, agem nesses dois casos? Isso que vamos responder, a seguir.
Quando o carrinho está em repouso, na altura , não é novidade pra ninguém que a única energia agindo é a potencial gravitacional. Em compensação, no topo do loop, o carrinho tem os dois tipos (cinética e potencial gravitacional), visto que está a uma altura da base a uma velocidade desconhecida.
Só nos resta então ir para as contas!
Passo 2
O que temos que fazer agora, é aplicar o princípio da conservação da energia mecânica para o nosso sisteminha. Como não há força de atrito nesse problema, logo a energia se conserva em todo percurso do carrinho. Isso quer dizer que a energia lá na altura , onde o carrinho parte do repouso é igual a energia no topo do loop ). Igualamos então, as duas energias:
Como a energia cinética é dada por
Passo 3
Agora que já sabemos a velocidade, podemos calcular a força que os trilhos exercem sobre o carrinho, de acordo com a figura abaixo:
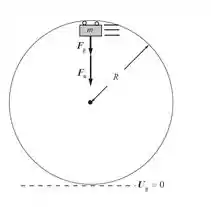
A força centrípeta, nada mais é do que a soma do peso do carrinho, , com a força normal, , exercida pelos trilhos sobre o carrinho. Vamos então, calcular .
E o raio do movimento circular é
Resposta
A força normal sobre os trilhos é aproximadamente igual a