Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 24
23. Responda os itens abaixo:
a) Encontre a força associada à função energia potencial , onde é uma constante.
b) Em que valores de a força é igual a zero ?
Passo 1
Para se resolver os seguintes itens é necessário atentar à relação que existe entre energia potencial e força. Fisicamente falando, para o caso de uma força e energia potencial na direção , é definido como o negativo da derivada da função de energia potencial em relação a , ou seja, Consequentemente, dado em função de , podemos encontrar , diferenciando em relação a .
Passo 2
a) Com base na fórmula já trabalhada anteriormente, bastar agora derivar a função de energia potencial em relação a , para encontrar a força desejada:
Como , substitui-se então da expressão da derivada:
Como é uma constante, então pula para fora da derivada. Resta então tirar a derivada em relação a de , que é bem simples:
Passo 3
b) Para encontrar os valores de a força é igual a zero basta igualar a força , obtida anteriormente a zero e observar em quais pontos a força anula-se, ou seja ou zeros da função:
Para observar em quais pontos a função acima anula-se, basta olhar o gráfico da função que a descreve, e ver para quais pontos de , seu valor é igual a zero:
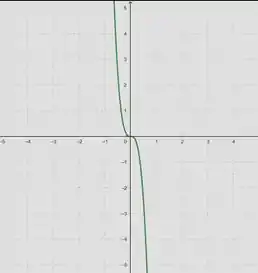
Logo para , uma vez que a função que descreve a força zera apenas nesse ponto
Resposta
a)
b)