Um carro de está se movendo inicialmente para o norte a no sentido positivo de um eixo . Depois de fazer uma curva de para a direita em , o motorista desatento bate em uma árvore, que para o carro em . Na notação de vetores unitários, qual é o impulso sobre o carro (a) devido à curva e (b) devido à colisão? Qual é o módulo da força média que age sobre o carro (c) durante a curva e (d) durante a colisão? (e) Qual é a direção da força média que age sobre o carro durante a curva?

Bom pessoal , nós sabemos que o impulso que age sobre o carro é dado por :

Dessa forma , como o momento inicial do carro após fazer a curva é e o momento final depois de colidir com a árvore , temos que :

Além disso nós sabemos que a força média que age sobre o carro enquanto está fazendo a curva é dada por :

e o módulo da força média pode ser calculado como já estamos acostumados :

Da mesma forma que no item anterior , a força média durante a colisão com a árvore é dada por :

e o módulo da força média é :

Como foi mostrado no item (c), a força média que age sobre o carro enquanto está fazendo a curva, na notação dos vetores unitários, é .

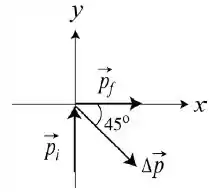
Reparem que enquanto o carro está fazendo a curva, a força média tem a mesma direção que e que . As componentes e de têm o mesmo valor absoluto, mas a componente é positiva e a componente é negativa. Assim, a variação de momento e a força média fazem um ângulo depara baixo com o semieixo x positivo, como mostra a figura abaixo.