A razão impulso-peso inicial de um foguete é , onde é o impulso do foguete e é sua massa inicial, incluindo o combustível. (a) Para um foguete lançado diretamente para cima, da superfície da terra, mostre que , onde é a aceleração inicial do foguete. Em um vôo tripulado, não pode ser maior do que 4 para conforto e segurança dos astronautas. (Quando o foguete é lançado, os astronautas se sente vezes mais pesados que o normal.) (b) Mostre que a velocidade final de um foguete lançado da superfície da Terra pode, em termos de e de (veja o problema 96), ser escrita como:
onde é a massa do foguete (não incluindo o combustível gasto). c) Usando uma planilha de calculo ou uma calculadora gráfica, faça o gráfico de em função da razão entre as massas , para e , com os valores da razão de massas variando de até . (Note que a razão de massas não pode ser menor do que 1.) (d) Para colocar um foguete em órbita, é necessária uma velocidade final quando da queima total. Calcule a razão de massas necessária para colocar em órbita um foguete de estágio único, usando os valores do impulso específico e da razão impulso-peso dadas na parte (c). Por questões de engenharia, é difícil construir um foguete com uma razão de massas muito maior do que . Isso lhe sugere por que foguetes de múltiplos estágios são normalmente usado para colocar cargas em órbita ao redor da Terra?
Passo 1
- A equação para a força que atua no foguete é:
No momento do lançamento:
Passo 2
b) A velocidade final pode ser calculada pela equação:
Onde é o tempo de queima.
Multiplicando em cima e embaixo por :
Substituindo isso em :
Do problema 96, . Substituindo e fatorando, obtemos:
Passo 3
c) Aqui, vamos precisar da ajuda das planilhas. Eu fiz aqui em um programa de planilhas jogando todos os dados que temos e ele montou esse gráfico.
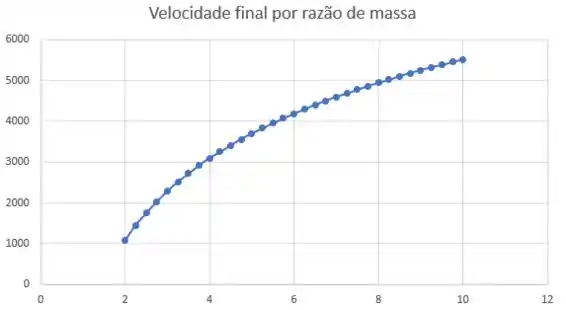
Passo 4
d) Substituindo os dados da parte (c) na equação que obtivemos na parte (b):
Para resolver isso, precisamos de uma calculadora gráfica. Jogando essa equação lá, vamos obter:
Que é um valor muito maior que o valor 10 dado como máximo possível pela questão.