Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 2.2 - Ex. 11
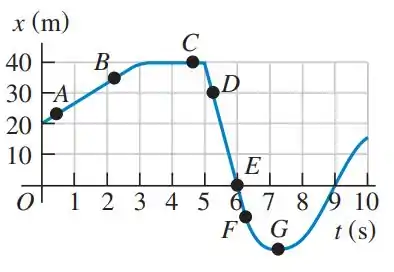
Um carro de testes trafega em movimento retilíneo pelo eixo Ox. O gráfico na Figura E2.11 mostra a posição x do carro em função do tempo. Determine sua velocidade instantânea nos pontos de A até G.
Passo 1
E aiii galera!
Tudo bom com vocês?
Vamos fazer mais uma questãozinha?
Bom... o enunciado nos dá o seguinte gráfico que descreve a distância em função do tempo :
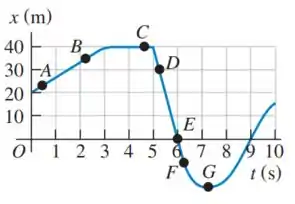
Queremos encontrar a velocidade instantânea usando o gráfico.
Bom... A velocidade instantânea em qualquer ponto é a inclinação do gráfico versus nesses pontos. Vamos estimar a inclinação do gráfico.
Passo 2
Começando pelos pontos e . De cara, podemos perceber que ambos os pontos pertencem a uma mesma reta. E para encontrar a inclinação de uma reta, só basta fazer:
Aqui eu vou fazer e , pois esses são pontos da reta que são fáceis de encontrar os valores, você não precisa necessariamente escolher o ponto final e inicial da reta, tá bem?
E a velocidade do ponto é a mesma por estar na mesma reta.
Passo 3
Já para o ponto , percebemos que ele está em uma reta horizontal. Isso significa que o corpo está parado, ele não está nem ganhando nem perdendo posição com o tempo.
Isso também pode ser visto pelo fato que , logo:
Passo 4
Já os pontos , e pertencem a uma mesma reta, que é decrescente. De cara, podemos perceber que a velocidade aqui nesses pontos será negativa, pois o corpo está perdendo posição com o tempo.
Vamos encontrar a inclinação dessa reta, aqui eu vou escolher e , que são pontos fáceis de encontrar dessa reta, lembra que eu disse que não precisava ser necessariamente o ponto final e o ponto inicial, portanto, a inclinação dessa reta é:
E essa é a velocidade para os pontos , e .
Passo 5
Com relação ao último ponto, o ponto (sem piadinhas de tiozão aqui rs)
Esse ponto ele está no vértice de uma parábola. Como encontrar a inclinação ali?
Bom, quem já viu alguma coisa de cálculo I, vai saber que ali é um ponto de mínimo, e que a derivada (também conhecida como inclinação) é zero.
Se você ainda não viu isso, pode pensar no seguinte, naquele ponto em específico, o carro está ganhando ou perdendo posição? Não dá pra dizer né... antes daquele ponto, o gráfico é decrescente e podemos ver que o carro perde posição com o tempo, e depois daquele ponto, o gráfico é crescente e podemos ver que o carro ganha posição o tempo. Naquele ponto em específico, ele não ganha nem perde, a realidade é que ali, o carro parou para alterar o sentido do seu movimento, e portanto, sua velocidade é zero.