Exercícios de Velocidade e Aceleração Instantânea - Lista de Exercícios Resolvida
Questão 1
A figura mostra a velocidade de uma partícula que se move em um eixo. O ponto É o ponto mais alto da curva; o ponto é o mais baixo; os pontos e estão na mesma altura. Qual é o sentido do movimento no instante t =0 e no ponto 4 ? Em qual dos seis pontos numerados a partícula inverte o sentido de movimento? Coloque os seis pontos na ordem do módulo da aceleração, começando pelo maior.
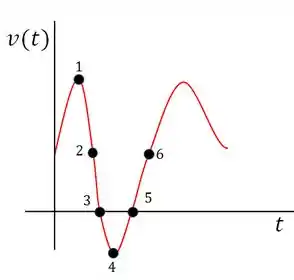
Questão 2
A aceleração de um corpo com movimento retilíneo é dada por , onde é uma constante positiva. Sabendo-se que, quando , e , obter a velocidade e a posição como funções do tempo. Obter também como função de .
Ver solução completaQuestão 3
Se a posição de uma partícula é dada por , onde está em metros e em segundos, em que instantes a velocidade da partícula é zero? Em que instantessa aceleração é zero? Para que intervalo de tempo positivo e negativo a aceleração é negativa? Para que intervalo de tempo positivo ou negativoa aceleração é positiva? Trace os gráficos de .
Ver solução completaQuestão 4
A velocidade escalar de um carro em uma pista reta é dada pela expressão:
Onde é medido em segundos e é medido em . Qual é a distância percorrida pelo carro no intervalo de tempo de a ?
a)
b)
c)
d)
e) nenhuma destas
Ver solução completaQuestão 5
Duas partículas se movem ao longo do eixo x. A posição da partícula 1 é dada por: onde x está em metros e t em segundos e a velocidade da partícula 2 é dada por onde a está em metros por segundo ao quadrado e t também em segundos.
a) Em que instante as partículas têm a mesma velocidade?
b) Qual a velocidade de A e B no t=0s?
Ver solução completaQuestão 6
A posição de um elétron que se move ao longo do eixo é dada por , onde está em segundos. A que distância está o elétron da origem quando para momentaneamente?
Ver solução completaQuestão 7
A posição de uma partícula que se move ao longo do eixo é dada em centímetros por , onde está em segundos. Calcule a velocidade média durante o intervalo de tempo de a a velocidade instantânea em a velocidade instantânea em a velocidade instantânea em a velocidade instantânea quando a partícula está na metade da distância entre suas posições em e Plote o gráfico de em função de e indique suas respostas graficamente.
Ver solução completaQuestão 8
A velocidade (em metros por segundo) de uma partícula que se move no plano xy é dada por:
a) Qual é a aceleração no instante t=3s?
b) Em que instante (se possível) a aceleração é nula?
c) Em que instante (se possível) a velocidade é nula?
Ver solução completaQuestão 9
A velocidade de uma partícula que descreve um movimento unidimensional é bem descrita pela seguinte expressão: . Calcule em que instante de tempo a partícula atinge sua velocidade máxima.
- 2,25s
- 1,1s
Questão 10
A grandeza “jeca” () é definida como a derivada da aceleração de um corpo:
Qual é o significado físico da área abaixo da curva ?
a) a aceleração do corpo.
b) mudança da taxa de aceleração do corpo.
c) não há dados suficientes para fazer qualquer afirmação.
d) a velocidade do corpo.
e) o deslocamento do corpo.
Ver solução completaQuestão 11
A velocidade escalar de um carro em uma pista reta é dada pela expressão:
Onde é medido em segundos e é medido em . Qual é a distância percorrida pelo carro no intervalo de tempo de a ?
a)
b)
c)
d)
e) nenhuma destas
Ver solução completaQuestão 12
O movimento de uma partícula é descrito pelo vetor posição:
Onde e são constantes que valem e .
a) Determine o módulo de para qualquer instante de tempo, e desenhe um gráfico da trajetória da partícula, ou seja, o caminho que a partícula faz no plano .
b) Determine o vetor velocidade e a aceleração .
c) Desenhe um gráfico das componentes e da velocidade da partícula como função do tempo.
d) Desenhe os vetores posição, velocidade e aceleração para .
Ver solução completaQuestão 13
A velocidade de uma partícula em movimento ao longo do eixo varia com o tempo de acordo com a expressão , onde medido em e em
a) Qual a aceleração média entre e ?
b) Qual a aceleração no instante ?
Ver solução completaQuestão 14
A velocidade escalar de um carro em uma pista reta é dada pela expressão: , onde é medido em segundos e é medido em . Qual a aceleração escalar do carro em ?
a)
b)
c)
d)
e)
Ver solução completaQuestão 15
Uma partícula descreve uma trajetória parabólica dada por . Se a trajetória em obedece à equação , qual o módulo de sua velocidade em ?
a) ;
b) ;
c) ;
d) ;
e) ;
Ver solução completaQuestão 16
Pardais: Equipamentos instalados em postes que fotografam e registram a velocidade dos veículos em excesso de velocidade.
Quando você passa por um pardal de e sua velocidade é , você é multado.
Por que?
(a) No momento em que a posição do seu carro passa pelo radar, sua aceleração instantânea é zero.
(b) Sua velocidade média é maior que a permitida.
(c) A variação da posição em relação ao tempo que você está desenvolvendo é maior que a permitida.
(d) Sua velocidade instantânea é maior que a permitida.
(e) Sua aceleração média foi suficiente para alcançar a velocidade permitida.
Ver solução completaQuestão 17
A coordenada de um objeto varia em função do tempo conforme a equação , onde está em metros e em segundos. A partícula está momentaneamente em repouso no instante:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 18
A posição de uma partícula em metros é descrita pelo vetor:
onde o tempo t é dado em segundos.
Qual é o vetor velocidade da partícula (em ) no instante ?
Questão 19
Um objeto está em movimento retilíneo para a direita. A resultante das forças que atuam sobre o objeto está orientada para a direita, mas o seu módulo está diminuindo com o tempo. Qual é a alternativa correta?
(A) O objeto continuará em movimento para a direita, com sua velocidade crescente.
(B) O objeto continuará em movimento para a direita, com sua velocidade decrescente.
(C) O objeto continuará em movimento para a direita com velocidade constante.
(D) O objeto atinge o repouso e então inicia o movimento para a esquerda.
(E) O objeto atingirá o repouso.
Ver solução completaQuestão 20
Uma partícula se move no eixo e tem sua posição em função do tempo descrita pela equação , sendo medido em metros e em segundos. Considerando que para a direita o movimento da partícula possui sentido positivo, assinale qual das alternativas abaixo é falsa.
a) A partícula está à direita da origem do eixo de referência em .
b) A posição da partícula depende linearmente do tempo.
c) A velocidade da partícula é constante e não nula.
d) A aceleração da partícula é nula em todos os instantes de tempo.
e) A partícula nunca estará à esquerda da origem do eixo de referência.
Ver solução completaQuestão 21
A aceleração de um corpo que se move ao longo de uma reta varia em função do tempo conforme a função . Considerando que no instante inicial, a velocidade inicial é de , quanto vale o deslocamento do corpo entre os instantess ?
Questão 22
Uma partícula se desloca ao longo do eixo e sua posição em cada instante de tempo é dada pela função , com o tempo dado em e a posição em . A velocidade instantânea da partícula no instante é:
(a) .
(b) .
(c) .
(d) .
(e) .
(f) .
(g) .
Ver solução completaQuestão 23
Se é o vetor posição de uma partícula, cujas coordenadas são dadas em metros e o tempo em segundos, determine o valor da coordenada do vetor aceleração em , quando .
A.
B.
C.
D.
E.
Ver solução completaQuestão 24
A função horária do espaço de um carro em movimento retilíneo uniforme é dada pela seguinte eexpressão: . Determine em que instante esse móvel passará pela posição .
- 8s
- 10s
- 25s
- 20s
- 15s
Questão 25
A posição de uma partícula em metros é descrita pelo vetor:
onde o tempo t é dado em segundos.
Qual é o vetor velocidade média da partícula (em) entre os instantes e ?
que a aceleração da partícula B vale:
Questão 26
Um objeto se movimenta ao longo do eixo e possui a componente de sua velocidade dada pela função , com o tempo dado em e a velocidade em . A aceleração instantânea do objeto no instante é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 27
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade e a aceleração da partícula em função do tempo
Questão 28
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade e a aceleração da partícula em função do tempo
Questão 29
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula alcança a altura máxima para .
Questão 30
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A altura máxima alcançada ().
Questão 31
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial Calcule:
- A velocidade média e a aceleração média entre os instantes e .
Questão 32
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula bate no solo ().
Questão 33
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade e a aceleração da partícula em função do tempo
Questão 34
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A altura máxima alcançada ().
Questão 35
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula alcança a altura máxima para .
Questão 36
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula bate no solo ().
Questão 37
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula bate no solo ().
Questão 38
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade e a aceleração da partícula em função do tempo
Questão 39
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade média e a aceleração média entre os instantes e .
Questão 40
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A altura máxima alcançada ().
Questão 41
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade e a aceleração da partícula em função do tempo
Questão 42
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula alcança a altura máxima para .
Questão 43
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A altura máxima alcançada ().
Questão 44
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula bate no solo ().
Questão 45
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula bate no solo ().
Questão 46
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A velocidade e a aceleração da partícula em função do tempo
Questão 47
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula alcança a altura máxima para .
Questão 48
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- A altura máxima alcançada ().
Questão 49
Uma partícula move-se no plano e a sua posição ( em metros) em função do tempo ( em segundos) é descrita pela função vetorial . Calcule:
- O instante de tempo em que a partícula alcança a altura máxima para .
Questão 50
Ao ser posicionada a uma distância de do centro de um prato giratório, o qual realiza duas voltas em , uma bolinha de não escorrega. Determine (c) o módulo e a orientação da força centrípeta que atua sobre a bolinha.
Obs.: todas as respostas devem estar em unidades do SI.
Dica da prof.: para determinar a orientação tanto da aceleração centrípeta quanto da força centrípeta, basta dizer se são radiais para dentro ou para fora da circunferência.
Ver solução completaQuestão 51
A velocidade de uma partícula é dada por onde está em metros por segundo e em segundos.
b) Determinar a expressão para e fazer os gráficos de e ;
Ver solução completaQuestão 55
Qual das seguintes situações não é possível?
A) Um corpo tem velocidade zero e aceleração diferente de zero.
B) Um corpo se move com velocidade que aponta para o norte e aceleração que aponta para o norte.
C) Um corpo se move com velocidade que aponta para o norte e aceleração que aponta para o sul.
D) Um corpo viaja com velocidade constante e aceleração que varia com o tempo.
E) Um corpo viaja com aceleração constante e velocidade que varia com o tempo.
Ver solução completaQuestão 56
A posição de uma pedra que cai do alto de um rochedo, a partir do repouso, é dada por , medida para baixo a partir da posição inicial .
b. Calcule e avalie esta derivada em .
Ver solução completaQuestão 57
1 - A posição de um objeto em função do tempo é dada por , onde e , sendo e dados em unidades do Sistema Internacional (SI). Qual é a velocidade instantânea do objeto no instante ?
A) B)C) D) E)
Ver solução completaQuestão 58
O vetor posição (em metros) de uma partícula em função do tempo (em segundos) é dado por:
Em que instante de tempo a partícula inverte o sentido do seu movimento?
Questão 59
2. Dois carros viajam ao longo de uma estrada reta e horizontal. Observa-se que a distância entre os carros está aumentando. Qual das seguintes afirmações é verdadeira?
- Necessariamente, a velocidade de cada está aumentando.
- Necessariamente, pelo um dos carros tem aceleração diferente de zero.
- Necessariamente, o carro que está na frente tem aceleração maior do que o carro que está atrás.
- Necessariamente, a velocidade do carro que está atrás está diminuindo.
- Ambos os carros podem ter a mesma aceleração.
Questão 60
(Cap 2 – Ex 21) A posição de uma partícula que se desloca ao longo do eixo varia com o tempo de acordo com a equação , onde está em metros e em segundos. Quais são as unidades (a) da constante e (b) da constante ? Suponha que os valores numéricos de e são e , respectivamente. (c) Em que instante a partícula passa pelo maior valor positivo de ? De a , (d) qual é a distância percorrida pela partícula e (e) qual é o deslocamento? Determine a velocidade da partícula nos instantes (f) , (g) , (h) e (i) . Determine a aceleração da partícula nos instantes U) , (k), (1) e (m) .
Ver solução completaQuestão 61
(Cap 2 – Ex 14) A função posição de uma partícula que está se movendo ao longo do eixo é , com em metros e em segundos. (a) Em que instante e (b) em que posição a partícula para (momentaneamente)? Em que (c) instante negativo e (d) instante positivo a partícula passa pela origem? (e) Plote o gráfico de em função de para o intervalo de a . (f) Para deslocar a curva para a direita no gráfico, devemos acrescentar a o termo ou o termo ? (g) Essa modificação aumenta ou diminui o valor de para o qual a partícula para momentaneamente?
Ver solução completaQuestão 62
Dizer que um movimento se realiza com uma aceleração escalar constante de , significa que:
(a) Em cada segundo a aceleração do móvel aumenta de .
(b) Em cada segundo o móvel se desloca .
(c) Em cada a velocidade aumenta de
(d) Em cada segundo a velocidade do móvel aumenta de s.
(e) A velocidade é constante e igual a
Ver solução completaQuestão 63
(Cap 2 – Ex 20) A posição de uma partícula que se move ao longo do eixo x é dada por , onde está em metros e em segundos. Determine (a) a posição, (b) a velocidade e (c) a aceleração da partícula em . (d) Qual é a coordenada positiva máxima alcançada pela partícula e (e) em que instante de tempo é alcançada? (f) Qual é a velocidade positiva máxima alcançada pela partícula e (g) em que instante de tempo é alcançada? (h) Qual é a aceleração da partícula no instante em que a partícula não está se movendo (além do instante )? (i) Determine a velocidade média da partícula entre e .
Ver solução completaQuestão 64
[ENUNCIADO COMUM ÀS QUESTÕES 1 e 2]
Dois carros (A e B) movem-se em pistas paralelas e têm gráficos de posição em função do tempo mostrados na Figura.
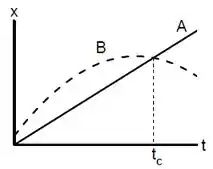
[QUESTÃO 2]
As equações horárias dos carros são e respectivamente, onde é medido em segundos e em metros. Determine em que instante os carros têm a mesma velocidade instantânea.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i) Nunca
Ver solução completaQuestão 65
- O gráfico abaixo mostra a posição (em metros) versus tempo (em minutos) de um objeto que se move ao longo de uma linha reta.
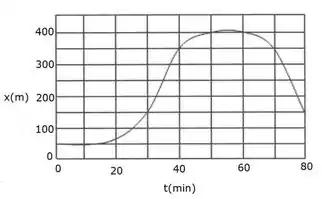
A velocidade instantânea do objeto no instante é mais próxima de
Questão 66
Dois carros, A e B, se deslocam em linha reta. A distância de A ao ponto de partida é dada como função do tempo por com . A distância de B ao ponto de partida com e
(c) Em que tempo(s) a distância de A e B não aumenta nem diminui?
Ver solução completaQuestão 67
A posição do parachoque dianteiro de um carro teste sob controle de um microprocessador é dada por :
Esboce os gráficos , e para o movimento do parachoque entre e .
Ver solução completaQuestão 68
Dois carros, A e B, se deslocam em linha reta. A distância de A ao ponto de partida é dada como função do tempo por com . A distância de B ao ponto de partida com e
(a) Qual carro está à frente logo após deixar o ponto de partida?
Ver solução completaQuestão 69
Dois carros, A e B, se deslocam em linha reta. A distância de A ao ponto de partida é dada como função do tempo por com . A distância de B ao ponto de partida com e
(b) Em que tempo(s) os carros estão no mesmo ponto?
Ver solução completaQuestão 70
Dois carros, A e B, se deslocam em linha reta. A distância de A ao ponto de partida é dada como função do tempo por com . A distância de B ao ponto de partida com e
(d) Em que tempo(s) A e B têm a mesma aceleração?
Ver solução completaQuestão 71
A posição do parachoque dianteiro de um carro teste sob controle de um microprocessador é dada por :
Encontre sua posição e aceleração nos instantes em que a velocidade do carro é nula.
Ver solução completaQuestão 72
As posições de um objeto em movimento bidimensional são dadas pelo vetor posição , onde todas as quantidades estão no sistema internacional de unidades. Qual é o ângulo que o vetor velocidade faz com o eixo no instante minuto?
Questão 73
A velocidade escalar de um carro em uma pista reta é dada pela expressão:
Qual é, aproximadamente, a aceleração do carro em ?
a)
b)
c)
d)
e) zero
Ver solução completaQuestão 74
O gráfico abaixo mostra a aceleração em função do tempo de um objeto que se move ao longo de uma linha reta partindo do repouso em . Com exceção do instante inicial , quando a velocidade do objeto será igual a zero?
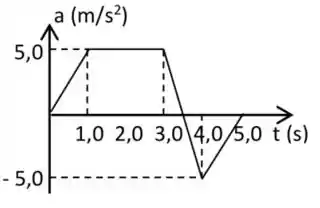
Questão 75
Um bloco de gelo com massa de está inicialmente em repouso sobre uma superfície horizontal sem atrito. A seguir, um trabalhador aplica uma força horizontal sobre ele. Como resultado, o bloco se move ao longo do eixo de tal modo que sua posição em função do tempo é dada por , onde e .
a) Calcule a velocidade do bloco quando
Ver solução completa
