Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.Problemas Adicionais - Ex. 78
Um próton está se movendo ao longo do eixo de acordo com a equação , onde está em metros e em segundos. Calcule (a) a velocidade média do próton durante os primeiros de movimento, (b) a velocidade instantânea do próton em e (c) a aceleração instantânea do próton em . (d) Trace o gráfico de em função de e mostre como a resposta do item (a) pode ser obtida a partir do gráfico. (e) Obtenha a resposrta do item (b) a partir do gráfico. (f) Trace o gráfico de em função de e mostre no gráfico a resposta do item (c).
Passo 1
(a) Primeiro vamos lembrar da definição de velocidade média:
Nesse caso, temos que considerar a variação da posição nos três primeiros segundos do movimento:
Podemos usar a função que foi dada no enunciado para calcular esses valores de :
Então:
Passo 2
(b) Agora queremos calcular a velocidade instantânea. Para isso precisamos derivar a função em relação ao tempo:
No instante :
Passo 3
(c) Agora, para encontrar a acelerçaão instantânea nesse mesmo instante, precisamos derivar mais uma vez em relação a :
Isso quer dizer que a aceleração é constante e igual a em qualquer instante de tempo.
Passo 4
(d) Agora queremos fazer o gráfico de , e usar esse gráfico para demonstrar o cálculo da velocidade média dos primeiros .
A função é , que corresponde a uma parábola com a concavidade para cima, e que passa pela a origem:
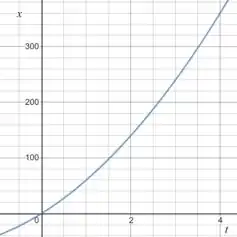
A velocidade média entre os pontos e corresponde à inclinação da reta que cruza esses dois pontos:
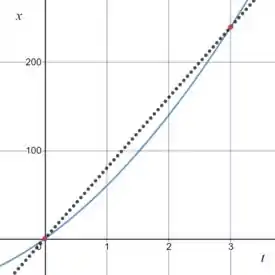
Para calcular a velocidade média entre nesse intervalo, você precisa calcular a inclinação dessa reta, então:
E ficamos com o mesmo resultado de antes:
Passo 5
(e) Agora queremos encontrar a resposta do item (b) a partir do gráfico. Ou seja, queremos a velocidade instantânea em .
Ou seja, queremos a velocidade instantânea em . Vimos que a velocidade instantânea é a derivada da função , ou seja, é a inclinação da reta tangente à curva nesse ponto:
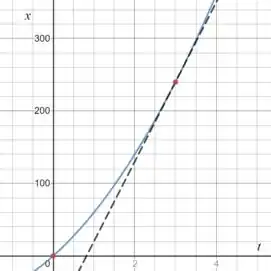
Passo 6
(f) Agora queremos fazer um gráfico da velocidade em função do tempo:
Esse é o gráfico de uma reta com inclinação e que cruza o eixo em :
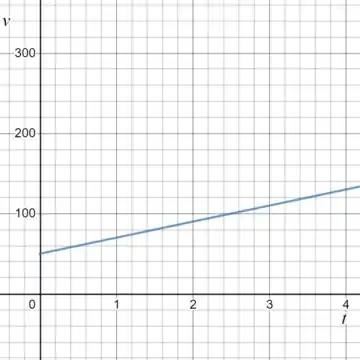
E queremos usar esse gráfico para calcular a aceleração do próton. Vimos que a aceleração é a derivada da função da velocidade.
Em outras palavras, a aceleração é a inclinação dessa reta. É só escolher dois pontos quaisquer no gráfico e calcular a inclinação:
Por exemplo, vamos tomar os pontos e :
Resposta
(a) .
(b) .
(c) .
(d) Ver gráfico.
(e) Ver gráfico.
(f) Ver gráfico.