Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 6.Problemas Adicionais - Ex. 88
Uma certa corda pode suportar uma tensão máxima de sem se partir. Uma criança amarra uma pedra de em uma das extremidades da corda e, segurando a outra extremidade, faz a pedra girar em uma circunferência vertical de de raio, aumentando lentamente a velocidade até a corda arrebentar. (a) Em que ponto da trajetória está a pedra quando a corda arrebenta? (b) Qual é a velocidade da pedra quanto a corda arrebenta.
Passo 1
(a) Vamos fazer um desenho da situação, representando o ponto mais baixo da trajetória.
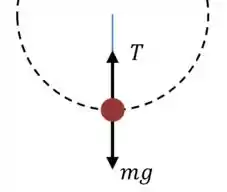
Nesse ponto, a força de tensão na corda tem que compensar totalmente o peso da pedra. Isos quer dizer que a força de tensão é máxima no ponto mais baixo da trajetória.
Como a corda se rompe a partir do momento em que a tensão ultrapassa um certo valor, a corda deve arrebentar justamente nesse ponto mais baixo.
Passo 2
(b) Agora vamos aplicar a segunda lei de Newton na pedra representada no nosso desenho.
Nesse caso, temos uma aceleração centrípeta apontando para cima (por isso aparece com sinal negativo), então:
Quando a corda se rompe, temos , então podemos calcular a velocidade:
Resposta
(a) A pedra está no ponto mais baixo da trajetória quando a corda arrebenta.
(b) A velocidade da pedra nesse instante é .