Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 10.Problemas - Ex. 10
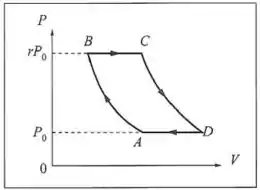
O ciclo de Joule, representado na figura abaixo, onde e são adiabáticas, é uma idealização do que ocorre numa turbina a gás: e representam respectivamente aquecimento e resfriamento a pressão constante; é a taxa de compressão. (a) Mostre que o rendimento do ciclo de Joule é dad por
(b) Calcule o rendimento para .
Passo 1
(a) Nosso primeiro objetivo é calcular o rendimento, que segue essa fórmula aqui:
E o primeiro passo pra fazer isso é usar a relação que vale para os processos adiabáticos:
Mas olhando o gráfico, dá pra ver que e :
Cortando e elevando os dois lados a :
Beleza, isso vai ajudar a calcular o trabalho realizado em cada trecho.
Passo 2
Nos trechos isobáricos, a fórmula do trabalho é essa aqui:
E nos trecho adiabáticos, a fórmula é essa:
Então, percorrendo o ciclo todo, vamos achar o seguinte:
Agora é a hora de usar as relações que a gente demonstrou no último passo:
Passo 3
O trecho em que o gás recebe calor é , e precisamos calcular essa quantidade . Uma boa ideia é usar a primeira lei da termodinâmica:
Ok, dá pra melhorar esse último termo:
Lembrando que
E além disso:
Substituindo isso:
Beleza, voltando pro cálculo do calor:
Passo 4
Agora vamos para o cálculo do rendimento, com certeza vai ser uma conta bem grande:
Onde é o trabalho total e é o calor absorvido pelo gás:
Vamos agrupar alguns termos no numerador:
Agora a gente pode cortar esse
E multiplicando tudo por :
Agora é só simplificar até chegar na forma do enunciado:
Pronto, demonstramos!
Passo 5
(b) Quando , o rendimento é:
E já que o gás é diatômico, , então:
Resposta
(a) Demonstração.
(b) .