Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 6.Problemas - Ex. 8
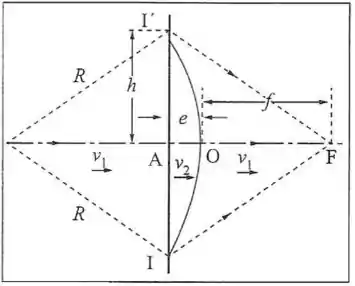
Uma lente esférica plano-convexa delgada é formada por um meio onde o som se propaga com velocidade , limitado por uma face plana e outra esférica de raio de curvatura ; o raio da face placa (figura) é suposto . No meio externo à lente, o som se propaga com velocidade , com , onde é o índice de refração relativo. Supomos . Nestas condições, uma onda plana incidente perpendicularmente sobre a face place é focalizada pela lente em seu foco . A distância do foco à face curva chama-se distância focal, e é a espessura da lente. (a) Mostre que para tem-se . Para isso, você poderá utilizar a aproximação: , válida para . (b) Com o auxílio do Princípio de Huygens, mostre que . Sugestão: Partindo da frente de onda plana incidente II’ (Figura). Iguale o tempo que as frentes de onda secundárias levam para convergir no foco passando pela periferia da lente (caminhos , ) e pelo centro (caminho ) e use o resultado da parte (a).
Passo 1
(a) Esse primeiro item parece muito complicado, mas na verdade só precisamos de um pouco de geometria plana:
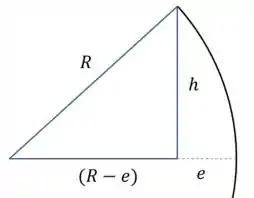
Pelo teorema de pitágoras:
E agora vamos usar a aproximação sugerida pelo enunciado, já que :
Que é exatamente o que queríamos demonstrar.
Passo 2
(b) Aqui podemos economizar bastante tempo utilizando a seguinte equação:
Onde são os índices de refração dentro e fora da lente, respectivamente, e e são os raios de curvatura de cada face.
No nosso caso, o índice de regração fora da lente é , já que estamos no ar, e o índice de refração dentro é simplesmente .
Para a face plano, consideramos que o raio de curvatura é infinito, então:
E o raio de curvatura da outra face é :
Ou seja:
Conforme queríamos demonstrar.
Resposta
(a) Demonstração.
(b) Demonstração.