Um cilindro com um pistão contém de oxigênio a uma pressão de e à temperatura de . Suponha que o oxigênio possa ser tratado como um gás ideal. O gas inicialmente se expande isobaricamente até ocupar um volume igual ao dobro do volume inicial. A seguir ele é comprimido isotermicamente de volta ao seu volume inicial e, finalmente, é resfriado isocoricamente até atingir sua pressão inicial. a) Desenhe um diagrama para essa sequência de processos. c) Calcule a pressão máxima. d) Calcule o trabalho total realizado pelo pistão sobre o gas nessa sequência de processos.
Passo 1
a) O esboço do diagrama é:
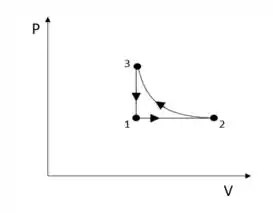
Passo 2
b) A compressão isotérmica é o processo de 2 para 3 no diagrama , podemos usar a temperatura final da expansão isobárica (1 para 2), que será a temperatura inicial da compressão isotérmica. Para isso, usamos a equação dos gases ideais para a expansão isobárica:
E como e são constantes:
Isolando :
Substituindo a temperatura do início e os volumes, já que o final é o dobro do inicial dados no enunciado:
Passo 3
c) A pressão máxima ocorre no final do processo isotérmico, vamos usar ele para encontrar ela, com a relação entre os processos final e inicial com a equação dos gases ideais:
Como nesse caso o processo é isotérmico, e o volume reduz pela metade em relação ao volume no inicio do processo:
A equação fica:
Simplificando, isolando e substituindo o valor de , que é a pressão no início do processo, que vai ser a mesma pressão que no início do processo anterior, já que ele era isobarico:
Passo 4
d) Para o processo isobárico, a pressão é constante e podemos usar o seguinte para calcular o trabalho:
Substituindo as temperaturas que calculamos na letra (b):
Para o caso do processo isotérmico, usamos a seguinte equação:
E como o volume final é metade do inicial nesse caso e a temperatura, que é constante, é a temperatura que calculamos no item (b), a equação fica:
E por fim, para o processo isocórico, o trabalho é zero, já que o volume é constante: