Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 19.Problemas - Ex. 60
A potencia do motor de um automóvel é diferetamente proporcional à massa de ar empurrada para dentro dos cilindros do motor para produzir uma reação química com a gasolina. Muitos carros possuem um turbocompressor que produz a compressão do ar antes de ele entrar no motor, fornecendo maior quantidade de massa por unidade de volume. Essa compressão rápida, essencialmente adiabática, também aquece o ar. Para aumentar ainda mais a compressão, o ar passa através de um inter-resfriador onde troca calor com duas vizinhanças à pressão constante. O ar é a seguir injetado nos cilindros. Em um mecanismo típico, o ar é conduzido ao turbocompressor sob pressão atmosférica , com densidade e a temperatura igual a . Ele é comprimido adiabaticamente até . No inter-resfriador ele é resfriado até sua temperatura original de a uma pressão constante de . a) Desenhe um diagrama para essa sequencia de processos. b) Se o volume de um dos cilindros for igual a , qual será a massa de ar proveniente d inter-resfriador que encherá um cilindro à pressão de ? Em comparação com a potencia de um motor que recebe ar a uma pressão e à temperatura de , qual é a porcentagem de aumento da potencia obtida usando-se um turbocompressor e um inter-resfriador? c) Caso o inter-resfriador não seja usado, qual deverá ser a massa de ar proveniente do turbocompressor que encherá um cilindro à pressão de ? Em comparação com a potencia de um motor que recebe ar a uma pressão de e a temperatura de , qual é a porcentagem de aumento de potencia obtida usando-se apenas turbocompressor?
Passo 1
Bom, galera,
A densidade do ar é dada por
Para um processo adiabático,
A equação para gases ideias é:
Usando na equação fornece
Passo 2
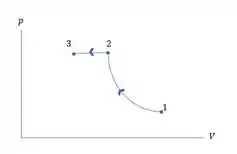
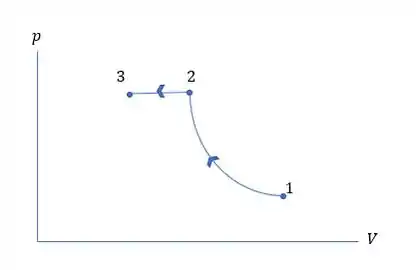
- O diagrama é esboçado a seguir:
- A temperatura final é igual à temperatura inicial e a densidade é proporcional à temperatura absoluta pressão. A massa necessária para encher o cilindro é então
- A temperatura após o processo adiabático é
Passo 3
Sem o turbocompressor ou o intercooler, a massa de ar a e em um cilindro é
O aumento da potência é proporcional ao aumento da massa de ar no cilindro; o aumento percentual é
Passo 4
A densidade se torna:
A massa de ar do cilindro é
O aumento percentual de energia é
O turbocompressor e o intercooler têm um efeito considerável na potência do motor.
