Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.10 - Ex. 65
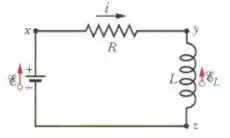
No circuito da Fig. 30-20, suponha que , e . A fonte ideal é ligada no instante . (a) Qual é a energia fornecida pela fonte durante os primeiros ? (b) Qual é a energia magnética armazenada no campo do indutor nesse intervalo? (c) Qual é a energia dissipada no resistor nesse intervalo?
Passo 1
E aí, tudo certinho? 😊
O problema fala de um circuito em série e pede para calcular a energia fornecida pela fonte e a energia armazenada no indutor nos primeiros segundos.
Para o item (a), vamos lembrar que
Já para calcular a energia armazenada no indutor, podemos aplicar a fórmula
E sabendo qual é a energia liberada pela fonte e a energia armazenada no indutor, podemos aplicar a lei da conservação de energia e dizer que a energia dissipada pelo resistor é dada por
Bora começar! 😁
Passo 2
A energia é a integral da potência no tempo. A potência fornecida pela fonte é
Mas neste circuito, vimos que a corrente é
Assim,
Portanto, a energia fornecida pela fonte será
Substituindo os valores apara a fem, e , com , obtemos
Tranquilo até aqui? 🤔
Passo 3
Agora vamos calcular a energia armazenada no indutor, que é dada por
Assim,
Substituindo os valores:
Bacana, não é? 😇
Passo 4
Para calcular a energia dissipada no resistor, poderíamos calcular a potência e integrar no tempo para obter a energia. Mas tem um truque bem simples que resolve nosso problema: conservação da energia!
A energia fornecida pela bateria deve ser igual a soma da energia armazenada no indutor com a energia dissipada no resistor:
Assim,
E aí! entendeu tudo? Responde Aí! 😉
