Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 11.Problemas - Ex. 6
No circuito magnético da figura, a secção reta é constante, a permeabilidade magnética do material é e a corrente na bobina de espiras é . Calcule o campo no braço central e o campo nos demais braços.
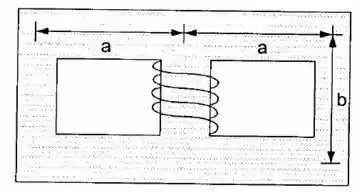
Passo 1
Vamos lá! Sabemos que o fluxo do campo magnético é dado por
Portanto
A relação entre o fluxo 1 e 2 é dada por
Passo 2
Tomando a figura, podemos escrever que
Sabendo que
podemos escrever que
Passo 3
Se liga, agora vamos recorrer aquela relação que encontramos antes , substituindo na equação anterior, teremos
Resposta
Exercícios de Livros Relacionados
Mostre que, no interior de uma ímã permanente (Seç. 11.8), podemos introduzir para o campo H → um novo potencial escalar magnético ξ tal que H → = - ∇ ξ , onde ξ está relacionado com a magnetização M
No problema anterior, a área da secção reta do anel é de 1c m 2 . Calcule:a) a energia armazenada no interior do ferro;b) a energia armazenada no entreferro;c) a auto-indutância do sistema.
Verifica-se que a contribuição máxima da magnetização do ferro ao valor de B no material é da ordem de 2 T . A massa atômica do ferro é 55,8 e sua densidade é 7,9g / c m 3 . a) Se cada elétron contrib
Como aplicação do problema anterior, considere um ímã permanente em forma de barra cilíndrica de raio a e comprimento l ≫ a . Nessas condições, podemos admitir, como aproximação, que a barra está unif
Exercício de Livro