Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 8.Problemas - Ex. 8
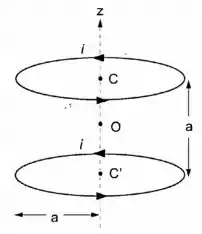
Duas bobinas circulares coaxiais idênticas, de espessura desprezível, com espiras de raio em cada bobina, transportam correntes de mesma intensidade e mesmo sentido, e estão colocados uma acima da outra, com seus centros e separados por uma distância (fig.) Considere o campo ao longo do eixo, na vizinhança do ponto médio do segmento , tomado como origem.
- Calcule B(O).
- Mostre que .
Daí resulta que esse dispositivo (bobinas de Helmholtz) produz um campo muito próximo de um campo uniforme na vizinhança da região central.
Passo 1
Se liga! A primeira coisa que precisamos lembrar para solucionar esta questão é que o campo produzido por uma espira é dado por
Onde representa o raio e é a distância do ponto ao centro da espira.
Levando em consideração que o comprimento para a espira de cima é
Temos que
Passo 2
Agora, para a espira de baixo, temos as mesmas condições e teremos um campo com a mesma magnitude da de cima.
Precisamos lembrar que como as espiras tem correntes em sentidos contrários, elas terão campo apontando na mesma direção. Portanto, basta somarmos os campos, ou seja, multiplicar por 2 o campo que já temos. Sendo assim, o campo total é
Pronto! Matamos o item (a)!
Passo 3
Agora, no item (b), precisamos mostrar que
Então, como o campo que encontramos no ponto é constante, podemos dizer que suas derivadas serão zero.