Como aplicação do problema anterior, considere um ímã permanente em forma de barra cilíndrica de raio e comprimento . Nessas condições, podemos admitir, como aproximação, que a barra está uniformemente magnetizada, ou seja, que dentro da barra é um vetor constante. Pela (11.8.21), a distribuição de ‘carga magnética’ equivalente tem densidade superficial constante nas duas extremidades circulares da barra (‘norte’ e ‘sul’) e é nula fora delas. Usando esse método, calcule : (a) no centro da barra; (b) no centro da face ‘norte’.
Passo 1
Antes de resolvermos o problema propriamente dito, vamos resolver um problema que parece completamente diferente: um cilindro de raio e altura com densidade de carga superficiel na face superior e na face interior, como mostrado na figura:
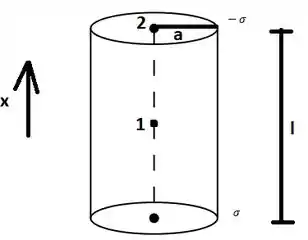
Queremos achar o campo elétrico no ponto 1 e no ponto 2. Para isso, você deve lembrar da fórmula do campo no eixo de um disco de raio a uma distância do plano:

Vamos olha primeiro para o ponto 1, no centro da barra. Devemos considerar tanto a carga na face da baixo como a carga de cima. Nos dois casos, o campo vai apontar para cima:
Portanto,
Agora vamos fazer a expansão para :
Lembrando que para , como , temos que
Portanto, o campo no centro da barra é
Passo 2
Agora vamos olhar para o ponto 2, na face superior. Mas aqui temos cuidado pois há uma descontinuidade do campo. Imediatamente acima da face ele terá um valor e imediatamente abaixo, outro. Vamos denotar por o campo acima e o campo imediatamente abaixo da face.
Vamos calcular primeiro . A contribuição da face superior será na direção com e a da face inferior será na direção com . Assim,
Ou ainda,
Para o campo imediatemnte acima, a única coisa que muda é que a contribuição da face superior passa a ser na direção , já que o campo é sempre atrativo com relação a essa face:
Portanto,
Note que
Como já é esperado, a descontinuidade do campo é a densidade de carga superficial acumalada na superfície dividida por .
Vamos tomar o caso limite com :
Portanto, resumindo nossos resultados para os campos:
Passo 3
Bom, você deve estar imaginando, o que essa conta do campo elétrico tem a ver com o problema que queremos resolver? Inicialmente não tem nenhuma ligação, mas a estrutura das equações é muito semelhante, de modo que podemos usar a mesma estrutura da solução! Foi isso que vimos no exercício 7!
No exercício 7 provamos que dentro de um ímã, podemos definir com
Note que essa estrutura é idêntica à equação de Poisson:
Note que está para , assim como está para . Portanto, pensando num ímã como um cilindro de raio e altura , com e com ‘cargas magnéticas’ na face superior e na face inferior, basta pegar as soluções para o problema da campo elétrico e trocar por :
Eu quis fazer primeiro com o campo elétrico porque sei que você tem mais familiaridade com ele 😊.
Antes de continuar, vamos pensar no que fazer com os dois valores no ponto 2 (face superior). O que os físicos muitas vezes fazem quando se deparam com descontinuidades desse tipo é tomar o valor sobre a superfície como sendo a média dos valores imediatamente e imediatamente abaixo:
Com isso, achamos
Passo 4
Mas nosso objetivo é achar , não . Para isso, vamos primeiro dar um jeito de colocar a magnetização no problema.
Vamos comparar a equação novamente:
Note que existe uma analogia entre e . O exercício pediu para consideramos a magnetização uniforme no interior do cilindro. Sendo assim, vamos fazer a analogia com o elétrico uniforme, que seria
Portanto, pela anologia, temos que
Com isso, podemos escrever:
Passo 5
Agora temos que relacionar com . Para isso, lembre-se que
Para o ponto no meio da barra, consideramos que a magnetização é é a magnetização uniforme no interior da barra. Assim,
Já para o ponto na face superior, consideramos a média entre a magnetização imediatamente acima com a magnetização imediatamente abaixo:
Logo,
Note que é a resposta do item (a) e é a resposta do item (b)!