Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 28.1 - Ex. 29

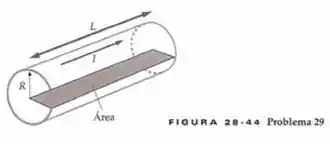
Um condutor cilíndrico longo com raio R e comprimento L conduz uma corrente I . Determine o fluxo magnético por unidade de comprimento através da área indicada na Figura 28-44.

Passo 1

E aí bonit@s, se liguem só que essa questão tem alguns detalhes que merecem destaque: Considere um elemento de área d A   =   L d r onde r   ≤   R . Podemos usar sua definição para expressar d ϕ m através desta área em termos de B e a lei de Ampère para expressar B como uma função de I . O fato de que a corrente é uniformemente distribuída sobre a área da seção transversal do condutor nos permite estabelecer uma proporção da qual podemos obter I como uma função de r . Com essas substituições no lugar, podemos integrar d ϕ m   para obter ϕ m / L .

Passo 2

Como B → é paralelo a n ^ em toda a área, assim, podemos expressar o fluxo d ϕ m através de uma seção L d r como

d ϕ m = B d a = B L d r       1

Aplicando a lei de Ampère vamos encontrar

∮ C B → ⋅ d l → = 2 π r B = μ 0 I c

Isolando B encontraremos

2 π r B = μ 0 I c → B = μ 0 I c 2 π r       2

Usando o fato de que a corrente I é uniformemente distribuída sobre a área da seção transversal do condutor, expressaremos sua variação com a distância r do centro do condutor:

I r I = π r 2 π R 2 → I r = I c = I r 2 R 2

Substituindo em 2 teremos

B = μ 0 ⋅ I r 2 R 2 2 π r = μ 0 I r 2 π R       3

Passo 3

Agora, vamos substituir 3 em 1 e já integrar em seguida de r = 0   a   r = R . Dessa forma, teremos

d ϕ m = μ 0 L I r 2 π R 2   d r

→ ϕ m = μ 0 L I 2 π R 2 ⋅ ∫ 0 R r   d r = μ 0 L I 4 π

Por fim, para acabarmos de vez com o problema vamos dividir ambos os lados por L de modo a obtermos

ϕ m L = μ 0 I 4 π

Pronto, tá resolvido nosso problema.

Resposta

ϕ m L = μ 0 I 4 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma espira quadrada é mantida em um campo magnético uniforme de 0,24 T perpendicular ao plano da espira. O comprimento dos lados do quadrado está diminuindo a uma taxa constante de 5,0 cm/s. Qual é a
Uma espira retangular de lados a e b afasta-se com velocidade v = vx ^ de um fio retilíneo muito longo, que transporta corrente contínua de intensidade I . A espira tem resistência R e autoindutância
Uma espira retangular de lados a e b de resistência R cai num plano vertical e atravessa uma camada onde existe um campo B uniforme horizontal (fig.).Repita o cálculo num instante posterior, em que a
No circuito indicado na Figura P29.47, uma fem de 90,0 V é acrescentada em série com o capacitor e o resistor, e o capacitor está inicialmente descarregado. A fem é Figura P29.47 colocada entre o capa
Uma barra metálica com 0,360 m é puxada para a esquerda por uma força aplicada F. A barra desliza sobre trilhos metálicos paralelos conectados através de um resistor de 45,0 V, como indica a Figura E2