Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 32.Problemas - Ex. 47
47- Um condutor cilíndrico com seção circular de raio e resistividade conduz uma corrente constante .
Determine o módulo, a direção e o sentido do vetor em um ponto imediatamente abaixo da superfície do fio situado a uma distância do eixo central.
Determine o módulo, a direção e o sentido do vetor nesse mesmo ponto.
Calcule o módulo, a direção e o sentido o vetor de Poynting nesse mesmo ponto. (O sentido de indica o sentido em que a energia eletromagnética flui para o interior ou para o exterior do condutor.)
Use o resultado do item para calcular a taxa de escoamento de energia para o interior do volume ocupado por um comprimento do condutor. (Sugestão: integra sobre a superfície do volume considerado.) Compare o resultado a taxa da geração de energia térmica do mesmo volume. Explique por que a energia dissipada na resistência de um condutor que conduz uma corrente pode ser interpretada em termos de uma energia que penetra no solenoide através de suas paredes cilíndricas.
Passo 1
O campo elétrico com o valor da resistividade do fio será calculado por:
Onde então:
Pois é o raio do fio. E ela é uniforme durante todo o raio do fio e tem direção no mesmo sentido que a corrente.
Passo 2
A questão não diz se esse fio tem a corrente entrando ou saindo da página né hahaha (isso considerando também a área da seção transversal do fio no plano da página), então vamos considerar aqui a corrente saindo da página o que pela regra da mão direita nos dá um vetor do campo magnético igual ao que está desenhado abaixo.
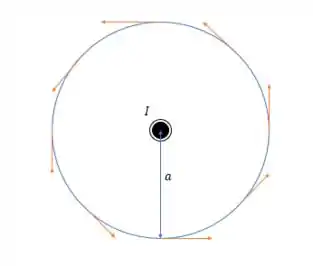
Onde todos os vetores tem intensidade e valem pela Lei de Ampere:
E como o ponto de interesse está abaixo do eixo central então o sentido desse vetor é apontando para a esquerda, caso a corrente esteja entrando no papel, o sentido será para a direita.
Passo 3
O módulo desse vetor será dado por:
E considerando ainda que o vetor é dado por:
E pela regra da mão direita para ondas eletromagnéticas (que é meio difícil explicar por palavras) nós temos que o sentido desse vetor é sempre apontando para dentro do fio de forma que temos.
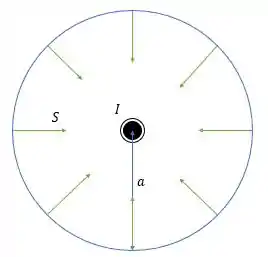
E se mudarmos a direção da corrente, tanto a direção do campo elétrico quanto do campo magnético irão inverter, nos dando uma mesma direção do vetor de apontar para o centro do fio.
Passo 4
Só de ler essa letra já dá uma canseira mas calma, o que ele quer é que calculemos a taxa de escoamento de energia do fio (o que é a potência) e a potência pode ser calculada pela intensidade.
Onde a área por assim dizer, será o comprimento do círculo de raio (pois é a nossa região de interesse).
Pois essa intensidade é a intensidade dentro de uma área circular, agora integrando essa região para um comprimento de fio nós iremos obter:
Só que a resistência de um fio cilíndrico de raio e comprimento é dado por , então: