Exercícios de Vetor de Poynting e Intensidade - Lista de Exercícios Resolvida

O vetor de Poynting associado com uma onda eletromagnética harmônica que se propaga no vácuo é dado por:

E é medido em .

1. Qual a direção e o sentido de propagação da onda? Justifique a sua resposta.
2. Suponha que em e no plano o campo elétrico aponte no sentido do eixo . Determine a expressão vetorial do campo elétrico associado a este vetor de Poynting.
3. Determine o vetor campo magnético associado com este vetor de Poynting.
4. Calcule o comprimento de onda e a frequência desta onda harmônica.

Frank D. Drake, um investigador do programa SETI (Search for Extra-Terrestrial Intelligence, ou seja, Busca de Inteligência Extraterrestre), disse uma vez que o grande radiotelescópio de Arecibo, em Porto Rico (Fig. 33-38), “é capaz de detectar um sinal que deposite em toda a superfície da Terra uma potência de apenas um picowatt”.

1. Qual é a potência que a antena do radiotelescópio de Arecibo receberia de um sinal como esse? O diâmetro da antena é .
2. Qual teria que ser a potência de uma fonte isotrópica situada no centro de nossa galáxia para que um sinal com essa potência chegasse à Terra?

O centro da galáxia fica a anos-luz de distância. Um ano-luz é a distância que a luz percorre em um ano.

O raio médio da Terra é de .

Uma onda eletromagnética plana tem o vetor campo magnético dado por

1. Determine: a direção e sentido de propagação da onda.
2. Determine o vetor campo elétrico associado a esta onda.
3. Calcule o vetor de Poynting.
4. Calcule a intensidade da onda.

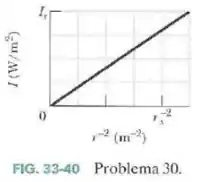
A intensidade da luz emitida por uma fonte pontual e isotrópica é medida em função da distância da fonte. A Fig. 33-40 mostra a intensidade em função do inverso do quadrado da distância, .

A escala do eixo vertical é definida por , e a escala do eixo horizontal é definida por .

Qual é a potência da fonte?

Podemos modelar de forma razoável uma lâmpada incandescente de como uma esfera de de diâmetro.

Tipicamente, somente cerca de 5% da energia vai para a luz visível; o restante vai, em grande parte, para a radiação infravermelha não visível.

1. Qual é a intensidade da luz visível (em ) na superfície da lâmpada?
2. Quais são as amplitudes dos campos elétrico e magnético nessa superfície, para uma onda senoidal com essa intensidade?

Um avião que se encontra a uma distância de de um transmissor de rádio recebe um sinal com uma intensidade de .

Determine a amplitude:

1. Do campo elétrico associado ao sinal na posição do avião.
2. Do campo magnético associado ao sinal na posição do avião.
3. Se o transmissor irradia uniformemente ao longo de um hemisfério, qual é a potência da transmissão?

Em uma onda de rádio plana o valor máximo do campo elétrico é .

Calcule:

1. O valor máximo do campo magnético.
2. A intensidade da onda.

Uma onda eletromagnética monocromática plana possui um campo magnético dado por

1. Escreva as equações vetoriais para e .
2. Calcule a intensidade da onda no ponto

O campo magnético de uma onda eletromagnética se propagando no vácuo é dado por . Expresse suas respostas apenas em termos de dados do problema e constantes universais.

1. Determine o vetor campo elétrico desta onda. Justifique sua resposta por meio de um esquema gráfico dos vetores pertinentes.
2. Determine o vetor de Poynting desta onda.
3. Determine a energia total transportada pela radiação através de uma área perpendicular à frente de onda durante um intervalo de tempo igual a 4 vezes o período da onda.

Uma fonte luminosa cilíndrica de comprimento L = 0,8 m possui potência P = 100W. A onda luminosa emitida incide sobre uma superfície cilíndrica coaxial com a lâmpada, distante r = 40 m. Em primeira aproximação, determine:

(a) O valor eficaz (rms) do vetor intensidade do campo elétrico .

(b) O valor eficaz (rms) do vetor campo de indução magnética .

Uma onda eletromagnética plana monocromática que se propaga no vácuo possui um campo elétrico descrito pela expressão onde e são constantes positivas.

Determina a direção e o sentido de propagação da onda. Calcule o comprimento de onda e a frequência da onda em função das constantes e .

Qual relação deve haver entre e para que satisfaça a equação de onda da luz se propagando no vácuo?

Determine o vetor em função de , , e da velocidade da luz no vácuo .

Calcule o vetor de Poynting instantâneo e a densidade de energia média desta onda.

Um aparelho de rádio encontra-se a de uma estação transmissora e recebe um sinal com uma intensidade de .

A potência da estação transmissora, supondo que ela irradie uniformemente em todas as direções, será igual a:

11. Nenhuma das anteriores

Considere as seguintes afirmações e indique o item correto:

1. A atmosfera terrestre é formada por moléculas que tem comportamento similar a de um dipolo elétrico.
2. A intensidade da radiação produzida por um dipolo elétrico é maior na direção de oscilação do dipolo.
3. Cores mais azuladas apresentam frequências de campo eletromagnético maiores que cores avermelhadas.

1. Apenas e estão corretas.
2. Apenas e estão corretas.
3. Todas estão corretas.
4. Apenas está correta.
5. Apenas e estão corretas.

Uma onda eletromagnética plana se propaga no vácuo com velocidade no eixo . O campo de indução magnética oscila no eixo com , e . Esse campo é representado pela expressão .

Determine a expressão do vetor campo elétrico a partir da equação de Maxwell:

Encontre o vetor de Poynting .

O campo elétrico de uma onda eletromagnética que se propaga no vácuo é dado pela fórmula

Em função dos dados do enunciado e das constantes fundamentais dadas no formulário (substitua os valores, por exemplo use m/s), calcule e responda o que se pede.

(a) Determine i) a direção o e o sentido de propagação, ii) o vetor número de onda, iii) a frequência e iv) o comprimento de onda da onda eletromagnética.

(b)Determine o vetor campo magnético da onda eletromagnética.

(c)Calcule o vetor de Poynting e a intensidade da onda eletromagnética.

Um feixe de luz laser monocromático incide normalmente sobre uma placa que absorve totalmente a radiação. O feixe tem intensidade e seção reta circular de raio .

(a) Calcule a amplitude do campo magnético do feixe.

(b) Calcule a energia média absorvida pela placa no intervalo de tempo .

(c) Calcule a energia eletromagnética média contida num comprimento do feixe.

Uma onda eletromagnética plana monocromática de comprimento de onda propaga-se no vácuo no sentido positivo do eixo . Seu campo elétrico oscila na direção e sua amplitude assume metade do seu valor máximo na origem do sistema de coordenadas no instante . Nos itens (a) e (b) abaixo, expresse suas respostas em termos de , , e .

(a) Escreva as expressões dos vetores campo elétrico e campo magnético associados a esta onda.

(b) Calcule o vetor Poynting.

(c) No instante , um elétron de carga está passando pela origem do sistema de coordenadas com velocidade , na direção e sentido do eixo . Calcule o vetor força que age sobre o elétron em devido a essa onda.

Um feixe laser cilíndrico possui potência . Seu feixe possui diâmetro de . Determine:

O valor eficaz (rms) do campo elétrico .

O valor eficaz (rms) do campo de induçãoo magnética .

Uma onda eletromagnética plana se propaga no vácuo com velocidade .

O campo de indução magnética está no eixo e tem , , , sendo dado por uma função cossenoidal dotada de uma constante de fase .

1. Determine a expressão do vetor campo elétrico a partir da equação de Maxwell .
2. Encontre o vetor de Poynting e intensidade () dessa onda.

Em um dado ponto do espaço e um instante de tempo, o vetor campo magnético de uma onda plana, linearmente polarizada e monocromática está na direção e sentido do vetor . O vetor de Poynting, no mesmo ponto e instante de tempo, vale . No ponto e instante considerados, determine a direção e o sentido do campo elétrico da onda.

a) .

b) .

c) .

d) .

Uma onda eletromagnética plana se propaga no vácuo com velocidade .

O campo de indução magnética possui , e , sendo dado por .

1. Determine a expressão do vetor campo elétrico a partir da equação de Maxwell .
2. Encontre o vetor de Poynting e intensidade () dessa onda.

– Um feixe laser cilíndrico possui potência . Seu feixe possui diâmetro de . Determine:

1. O valor eficaz (rms) do campo elétrico .
2. O valor eficaz (rms) do campo de indução magnética .

Uma onda eletromagnética plana se propaga no vácuo com velocidade no eixo . O campo elétrico oscila no eixo com , e .

Esse campo é representado pela expressão

1. Determine a expressão do vetor de indução magnética a partir da equação de Maxwell .
2. Encontre o vetor de Poynting .

Uma onda eletromagnética tem uma frequência e se propaga no vácuo, com campo magnético . O eixo tem direção e o eixo tem direção . Qual das alternativas abaixo corresponde ao vetor de Poyting e o valor médio do vetor de Poyting (I)? Use a velocidade da luz e a permeabilidade magnética para dar a resposta do módulo do vetor de Poyting e o valor médio do vetor de Poynting em , e outras quantidades físicas relacionadas à onda eletromagnética em unidades . [Considere nas alternativas que os números no argumento da função estão nas unidades e para as variáveis e respectivamente].

1. Nenhuma das alternativas;
2. se propagando no sentido do eixo negativo e
3. se propagando no sentido do eixo positivo e
4. se propagando no sentido do eixo positivo e
5. se propagando no sentido do eixo negativo e
6. se propagando no sentido do eixo positivo e
7. se propagando no sentido do eixo positivo e

Uma fonte pontual emite ondas eletromagnéticas esféricas e monocromáticas. A intensidade da onda a de distância da fonte vale .

Determine (i) a potência da fonte e (ii) a intensidade dessa onda a de distância da fonte.

1. e
2. e
3. e
4. e
5. e

O campo elétrico de uma onda eletromagnética que se propaga no vácuo é dado pela fórmula

Em função dos dados do enunciado e de constantes fundamentais dadas no formulário (folha de capa), calcule e responda o que se pede.

(a) Determine i) a direção e o sentido de propagação, ii) o vetor número de onda, iii) a frequência iv) o comprimento de onda da onda eletromagnética.

(b) Determine o vetor campo magnético (x, y, z, t) da onda eletromagnetica.

(c) Calcule o vetor de Poynting e a intensidade da onda eletromagnética.

Formulário:

- Média de seno e cosseno

Em certa região do espaço, o campo magnético de um feixe luminoso é dado por

, em unidades do SI. Para esta onda, determine:

(a) A frequência angular.

(b) O vetor campo elétrico.

(c) A intensidade.

(d) O vetor de Poynting.

O campo elétrico de uma onda eletromagnética plana monocromática que se propaga no vácuo é dado por , onde e são constantes.

(a) (0,5 ponto) Determine a direção e o sentido de propagação da onda. Calcule o comprimento de onda e a frequência desta onda em função das constantes e .

(b) (0,5 ponto) Que relação deve haver entre e para que o campo satisfaça a equação de ondas eletromagnéticas no vácuo?

(c) (0,5 ponto) Expresse o campo magnético em função de , , e da velocidade da luz no vácuo .

(d) (1,0 ponto) Calcule o vetor de Poynting instantâneo e a densidade de energia média desta onda.

A componente magnética da radiação existente no vácuo é dada pela superposição de duas ondas planas (SI):

Coloque a velocidade da luz m/s e se necessário deixe suas respostas em função de .

(a) (1,0 ponto) Calcule o número de onda e o vetor velocidade de propagação de cada componente de .

(b) (1,0 ponto) Determine as correspondentes componentes elétricas e .

(c) (1,0 ponto) Calcule o vetor de Poynting associado a esta radiação.

(d) (1,0 ponto) Esta radiação transporta energia? Justifique.

Uma onda eletromagnética plana tem o vetor campo magnético dado por

1. Determine: a direção e sentido de propagação da onda.
2. Determine o vetor campo elétrico associado a esta onda.
3. Calcule o vetor de Poynting.
4. Calcule a intensidade da onda.

Considere uma onda eletromagnética plana que se propaga no vácuo com campo elétrico dado por .

(a) Escreva a expressão para o campo magnético correspondente, justificando sua resposta.

(b) Calcule o vetor de Poynting e a intensidade da onda.

(c) Suponha que essa onda incide normalmente sobre um disco, de raio , perfeitamente absorvedor. Calcule a energia que atravessa o disco num intervalo de tempo igual ao período da onda.

Uma onda plana eletromagnética linearmente polarizada, propagando-se no vácuo no sentido positivo do eixo z, tem comprimento de onda e intensidade .

(b) Obtenha a expressão para o campo magnético

Uma onda eletromagnética circularmente polarizada e monocromática possui o vetor de Poynting dado por . A intensidade, a direção e o sentido de propagação dessa onda valem, respectivamente:

1. e .
2. e .
3. e .
4. e .
5. e .

Considere as sentenças a seguir sobre uma onda eletromagnética plana, linearmente polarizada e monocromática que se propaga no vácuo. Nessa situação, pode-se afirmar que

a) o vetor de Poynting é PARALELO ao vetor número de onda da onda eletromagnética.

b) o módulo do vetor de Poyting é IGUAL à densidade de energia eletromagnética da onda.

c) o vetor campo elétrico é PARALELO ao vetor campo magnético.

d) a densidade de momento linear da onda é NULA em todos os pontos do espaço-tempo.

Uma lâmpada de emite 50% de ondas eletromagnéticas uniformes. Calcular a intensidade da radiação eletromagnética a da lâmpada.

– Uma fonte luminosa cilíndrica de comprimento possui potência . A onda luminosa emitida incide sobre uma superfície cilíndrica coaxial com a lâmpada, distante .

Em primeira aproximação, determine:

1. O valor eficaz (rms) do vetor intensidade do campo elétrico .
2. O valor eficaz (rms) do vetor campo de indução magnética .

Uma onda eletromagnética plana de comprimento de onda se propaga no vácuo com velocidade no sentido positivo do eixo . O campo de indução magnética oscila no eixo com valor máximo de .

1. Calcule os valores do número de onda e da frequência angular . Escreva a função do vetor campo de indução magnética na forma senoidal em termos dos dados fornecidos. Considere a constante de fase nula.
2. Determine a função do vetor campo elétrico , sabendo que , onde designa o produto vetorial e designa o vetor unitário na direção da velocidade da onda.
3. Encontre a função do vetor de Poynting e a intensidade () dessa onda.

– Uma fonte luminosa cilíndrica de comprimento possui potência . A onda luminosa emitida incide sobre uma superfície cilíndrica coaxial com a lâmpada, distante .

Em primeira aproximação, determine:

1. O valor eficaz (rms) do vetor intensidade do campo elétrico .
2. O valor eficaz (rms) do vetor campo de indução magnética .

Um radar operando a com potência de tenta detectar, a uma distância de , um avião que se aproxima.

Suponha que o feixe de radar é emitido uniformemente através de um hemisfério.

1. Qual é a intensidade do feixe no local do avião?

O avião reflete as ondas de radar como se a área de sua seção transversal fosse somente .

2. Qual a potência do feixe refletido pelo avião?

Suponha que o feixe é refletido uniformemente através do hemisfério. Retornando ao local do radar, qual são:

3. A intensidade
4. O valor máximo do campo elétrico do feixe refletido pelo radar.

Um grande solenoide com espiras por unidade de comprimento tem uma corrente que aumenta lentamente com o tempo.

O solenoide tem raio e a corrente no enrolamento tem a forma , sendo a uma constante.

1. Encontre o campo elétrico induzido a uma distância do eixo do solenoide.
2. Encontre o vetor de Poynting na superfície do cilindro , logo abaixo do enrolamento do solenoide.
3. Calcule o fluxo do vetor de Poynting em um cilindro de comprimento e mostre que este é igual à taxa de variação da energia magnética do solenoide.

Dada a onda eletromagnética

Onde é uma constante.

1. Ache o campo magnético.
2. Ache o vetor de Poynting.
3. Calcule a intensidade da onda no ponto

Nikola Tesla, um inventor do Século XIX, propôs a transmissão de potência elétrica através de ondas eletromagnéticas senoidais.

Considere a potência elétrica transmitida por um feixe com seção reta de área igual a .

Qual deveria ser a amplitude do campo magnético e a amplitude do campo elétrico para que esse feixe pudesse transmitir uma potência elétrica comparável com a potência transmitida por uma linha de transmissão moderna (que operam com tensões da ordem de e correntes da ordem de )?

1. ;
2. ;
3. ;
4. ;
5. Nenhuma das anteriores

Uma lâmpada pontual emite luz (considere sendo uma onda plana emitida em todas as direções) com uma potência de .

Considere um ponto a uma distância de da lâmpada. Neste ponto, o campo elétrico em é:

Uma onda eletromagnética propaga-se numa região do espaço delimitada por dois planos condutores paralelos com equações e . Nesta região, o campo elétrico da onda é:

1. Determine a relação que deve haver entre , e para que o campo elétrico satisfaça a equação de ondas tridimensional.
2. A partir da forma diferencial da lei de Faraday determine o campo magnético associado ao campo elétrico dado.
3. Determine o vetor de Poynting no instante em um ponto com coordenadas , e .

4 – O campo elétrico de uma onda eletromagnética plana se propaga no vácuo é dado por .

a) Determine o vetor campo magnético desta onda.

b) Determine o vetor de Poynting desta onda.

c) Considerando que a onda incide normalmente sobre um disco perfeitamente absorvedor de raio , calcule a energia transferida ao disco durante um intervalo de tempo correspondente a periodos. Expresse sua resposta em termos das grandezas dadas acima.

Uma onda eletromagnética plana monocromática, com polarização linear e com frequência , se propaga no vácuo tal que seu vetor de Poynting está no sentido e tem amplitude máxima igual a na origem, para .

a) Escreve a expressão para o vetor de Poynting, em função do tempo e do espaço.

b) Sabendo que a polarização está no eixo e que o campo elétrico é positivo na origem para , escreva a expressão para o campo magnético, em função do tempo e do espaço.

c) A lei de Ampère, em sua formulação original, está dada por ou (em sua forma diferencial). Mostre que, escrita desta maneira, a Lei de Ampère não contempla situações fora da magnetostática (densidades de corrente variáveis).

d) A partir da Lei de Gauss na forma integral, chegue à sua formulação da forma diferencial.

– Uma lâmpada incandescente em forma de bulbo (gota) possui potência . Determine:

1. O valor eficaz (rms) do campo elétrico a uma distância de .
2. O valor eficaz (rms) do campo de indução magnética .

Um avião se encontra a 10 km de um transmissor de rádio. Ele recebe um sinal eletromagnético com o campo elétrico eficaz provindo desse transmissor. Considere o sinal chegando ao avião na forma de uma onda plana. Encontre a potência de transmissão (P) se a irradiação é feita em uma semiesfera.

O vetor de Poynting de uma onda eletromagnética plana, monocromática e linearmente polarizada é dado por .

A intensidade e a direção de propagação da onda são dadas por?

1. e
2. e
3. e
4. e
5. e
6. e
7. O vetor de Poynting dado não é fisicamente válido.

Uma lâmpada de potência média gera um campo elétrico de amplitude , em um dado ponto de observação. A lâmpada é substituída por outra mais eficiente com potência média . Determine o novo valor da amplitude do campo elétrico , no mesmo ponto de observação.

a) .

b) .

c) .

d) .

Uma onda eletromagnética monocromática plana possui um campo magnético dado por

1. Escreva as equações vetoriais para e .
2. Calcule a intensidade da onda no ponto

Uma onda eletromagnética plana de comprimento de onda 10,0 cm se propaga no vácuo com velocidade no sentido positivo do eixo x. O campo de indução magnética oscila no eixo OZ com valor máximo de 8,00 x Tesla.

(a) Calcule os valores do número de onda k e da frequência angular ω. Escreva a função do vetor campo de indução magnética na forma senoidal em termos dos dados fornecidos. Considere a constante de fase nula.

(b) Determine a função do vetor campo elétrico , sabendo que , onde x designa o produto vetorial e designa o vetor unitário na direção da velocidade da onda (cujo módulo é c).

(c) Encontre a função do vetor de Poynting S(x,t) e a intensidade (I) dessa onda.

Considere uma onda plana monocromática cujo vetor de Poynting é e o campo elétrico, . Obtenha o campo magnético dessa onda, onde os versores unitários , e formam, nessa ordem, um conjunto cartesiano de vetores.

(a)

(b)

(c)

(d)

(e)

(f)

A intensidade da luz solar ao chegar em nosso planeta Terra vale aproximadamente. Supondo que essa intensidade é a de uma onda plana, monocromática, e linearmente polarizada, determine a potência média de irradiação solar se a distância média Sol-Terra vale aproximadamente.

(a)

(b)

(c) 3