Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 30.1 - Ex. 55

Um condutor no formato de um longo cilindro solido com comprimento L,raio a e resistividade p,conduz uma corrente estacionaria/que esta uniformemente distribuida na sua secao transversal.(a)Use a lei de Ohm para relacionar o campo elétrico E no condutor a l,pea.(b)Determine o campo magnetico B no lado de fora do condutor.(c)Use os resultados da Parte(a)e da Parte(b)para calcular o vetor de Poynting S=(ExB)/u.emr ＝a(a borda do condutor).Em que direcao e sentido esta S?(d) Determine o fluxoS,dA atraves da superficie do cilindro e use o fluxo para mostrar que a taxa de tluxo de energia para dentro do condutoreFR,onde Rea resistencia do cilindro.

Passo 1

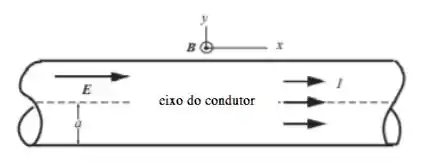
Uma vista lateral do condutor cilíndrico é mostrada no diagrama. Deixe a corrente estar à direita (na direção +x) e escolha um sistema de coordenadas em que a direção +y seja radialmente para fora do eixo do condutor. Então a direção +z é tangente às superfícies cilíndricas que são concêntricas com o eixo do condutor condutor (fora do plano do diagrama no local indicado no diagrama). Podemos usar a lei de Ohm para relacionar a intensidade do campo elétrico E no condutor a I, ρ , e a e a lei de Ampère para encontrar a intensidade do campo magnético B logo fora do condutor. Conhecendo E →  e  B → , podemos encontrar   S → , usando seu componente normal, mostrar que a taxa de fluxo de energia para o condutor é igual a I 2 R , onde R é a resistência.

Passo 2

Letra a:

Aplique a lei de Ohm ao condutor cilíndrico para obter:

V = I R = I ρ L A = I ρ π a 2 L = E L   o n d e     E = I ρ π a 2 E = I ρ π a 2

Passo 3

Letra b:

A aplicação da lei de Ampère a um caminho circular de raio a na superfície do condutor cilíndrico produz:

∫ C   B → ⋅ d l → = B ( 2 π a ) = μ 0 I   = μ 0 I B = μ 0 I 2 π a B → = μ 0 I 2 π a θ ^

Passo 4

Letra c:

O vetor de Poynting é dado por:

S → = 1 μ 0 E → × B → S → = 1 μ 0 I ρ π a 2 i ^ × μ 0 I 2 π a k ^ = - I 2 ρ 2 π 2 a 3 j ^ S ˙ = - I 2 ρ 2 π 2 a 3 r ^

Passo 5

Letra d:

O fluxo através da superfície do condutor para o condutor é:

∮ S n d A = S ( 2 π a L )

Substitua S n , o componente interno de S →   , e simplifique para obter:

∮ S n d A = I 2 ρ 2 π 2 a 3 ( 2 π a L ) = I 2 ρ L π a 2

Como R = ρ L A = ρ L π a 2 ,

∮ S n d A = I 2 R

Observações: A igualdade das duas taxas de fluxo é uma declaração da conservação de energia.

Resposta

  1. E = I ρ π a 2
  2. B → = μ 0 I 2 π a θ ^
  3. S ˙ = & - I 2 ρ 2 π 2 a 3 r ^
  4. ∮ S n d A = I 2 R
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma fonte de luz intensa irradia uniformemente em todas as direções. A uma distância de 5,0 m da fonte, a pressão de radiação sobre uma superfície perfeitamente absorvedora é 9,0 106 Pa. Qual é a potê
Segurança do laser. Se o olho humano receber uma intensidade média maior que 1,0 102 W/m2 , pode haver danos à retina. Essa quantidade é denominada patamar de dano da retina. (a) Qual é a maior potênc
Dobrar a frequência de uma onda na faixa de 25 Hz a 3 kHz representa que variação na intensidade máxima permitida de onda eletromagnética? (a) Um fator de 2; (b) um fator de 1/ !2; (c) um fator de 1 2
Uma fonte de ondas eletromagnéticas senoidais irradia uniformemente em todas as direções. A 10,0 m dessa fonte, a amplitude do campo elétrico é medida como 3,50 N/C. Qual é a amplitude do campo elétri
Visto que a velocidade da luz em um vácuo (ou no ar) possui um valor muito alto, ela é muito difícil de ser medida diretamente. Para medir essa velocidade, você realiza um experimento no qual mede a a