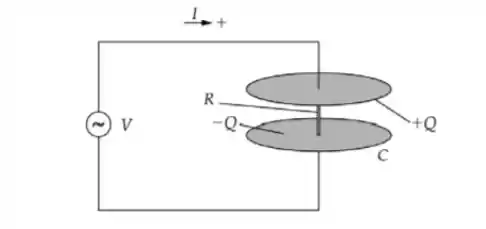
Um capacitor de placas paralelas tem placas circulares de raio a separadas por uma distancia d.No espacamento entre as duas placas estd um fino fio retilineo de resistencia R que conecta os centros das duas placas.Uma tensio dependente do tempo dada por Vosen ot e aplicada nas placas.(a)Qual e a corrente consumida no capacitor?(b)Qualeo campo magnetico como funcao da distancia radialr ate a linha central no interior das placas do capacitor?(c) Qual co angulo de fase entre a corrente consumida no capacitor e a tensio aplicada?
Passo 1
Parte da carga que entra no capacitor passa através do fio resistivo enquanto o resto se acumula na placa superior. A corrente total é a taxa na qual a carga passa pelo fio resistivo mais a taxa na qual ela se acumula na placa superior. O campo magnético entre as placas do capacitor é devido tanto à corrente no fio resistivo quanto à corrente de deslocamento embora uma superfície delimitada por um círculo a uma distância r do fio resistivo. A diferença de fase entre a corrente consumida pelo capacitor e a tensão aplicada pode ser calculada usando um diagrama fasorial.
Passo 2
Letra a:
A corrente puxada pelo capacitor é a soma da corrente de condução através do
fio de resistência e , onde Q é a carga na placa superior de o capacitor:
Expresse a corrente de condução Ic em termos da diferença potencial entre as placas e a resistência do fio:
Já que:
Substituindo na equação:
A capacitância de um capacitor de placa paralela com área de placa A e separação de placa d é dada por:
Substituindo C na equação da corrente, a gente tem que;
Passo 3
Letra b:
Aplique a forma generalizada da lei de Ampère a um caminho circular de raio r centrado dentro das placas do capacitor, onde , é a corrente de deslocamento através da superfície plana S limitada pelo caminho e é a corrente de condução através da mesma superfície:
Por simetria, a integral de linha é 8 vezes a circunferência do círculo de raio r:
Na região entre as placas do capacitor há um campo elétrico uniforme devido às cargas superficiais +Q e - Q. A corrente de deslocamento associada através de S é:
Para avaliar a corrente de deslocamento, primeiro devemos avaliar em todos os lugares em S. Perto da superfície de um condutor, onde é a densidade de carga superficial:
Então,
Substituindo por na equação por temos:
Resolvendo na equação (3) e substituindo e temos:
Passo 4
Tanto a carga quanto a corrente de condução estão em fase com . No entanto, , que é igual à corrente de deslocamento em S para , atrasa em 90 °.Matematicamente, é atrasado em 90º quando comparamos com A tensão é relacionada com a corrente pelo ângulo de fase . A relação de corrente é expressa em termos das amplitudes de corrente:
Os valores das amplitudes das correntes de condução e deslocamento são obtidos por comparação com a resposta da Parte (a):
E
Um diagrama fasorial para adicionar as correntes e é mostrado à direita. A corrente de condução está em fase com a tensão V através do resistor e está atrasado em 90°: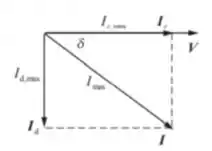
A partir do diagrama fasorial, temos:
Então,
Observações: O capacitor e o fio resistivo são conectados em paralelo. A diferença de potencial em cada um deles é a tensão aplicada .