Considere um solenóide de raio e comprimento , com espiras por unidade de comprimento, percorrido por uma corrente . Tome a origem no centro do solenóide, com eixo ao longo do eixo de simetria do cilindro. (a) Calcule a magnitude de do campo magnético num ponto do eixo à distancia do centro, tanto dentro como fora do solenoide. Quais os valores no centro e nas extremidades? (b) Obtenha e interprete o comportamento do para , . (c) Com , trace um gráfico de em função de para . Sugestão: Obtenha o campo do solenóide somando (integrando) o campo das espiras circulares ao longo do eixo.
Passo 1
Para resolvermos, vamos aceitar a querida sugestão do enunciado de como obter o campo no solenoide e iremos integrar para todo o objeto. Após isso vamos aplicar as condições de contorno para dentro e fora do solenoide. No item (b), vamos precisar utilizar uma expansão binomial para entendermos o comportamento da nossao função para os casos dados.
Passo 2
- Bom, vamos começar integrando para encontrar nosso campo para o solenoide. Se supormos que a corrente está no sentido anti-horário, mais ou menos como no esquema a seguir.
- Para e , vamos aplicar a expansão binomial, na qual
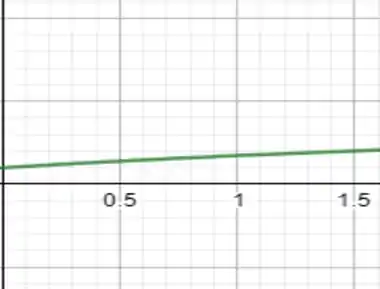
- Plotando o gráfico, vamos ter algo do tipo
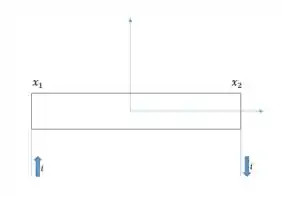
Mais ou menos assim só que bem desenhado. Temos então, fazendo a regra da mão direita, que o campo gerado está sendo apenas na direção , assim nossa variação da corrente é dada por
onde é o número de espiras. Nossa gaussiana que melhor servirá para resolver o problema será uma circunferência, assim, como teremos apontando apenas na direção , nosso caminho poderá ser escrito como . Usando Bio-Savart, temos que
Onde . Se integrarmos agora de até , vamos ter que
Se chamarmos , teremos que nossa integral fica
Temos que esses dois extremos, e será sempre pra direita ou esquerda, porém teremos sempre que subtrair a posição arbitrária do ponto, com coordenada . Assim, temos que
e
Substituindo na equação que , chegamos então que
Dentro do solenoide, teremos que , assim teremos que, como visto no livro para dentro de um solenoide, . Para , vamos ter que
Como , vamos ter que
Passo 3
Aplicando para nossa equação, vamos ficar com a expressão
e
Como , vamos ter que podemos reduzir para
e
Assim, com algumas manipulações, chegamos que nossa equação fica
Onde é o momento de dipolo magnético do solenoide.
Passo 4