Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 3.Problemas - Ex. 7a
Uma carga puntiforme é colocada numa caixa cúbica de aresta . Calcule o fluxo do campo elétrico sobre cada uma das faces se a carga ocupa o centro do cubo.
Passo 1
Se liga!
Precisamos lembrar que o fluxo é
Quando colocamos a carga no centro, temos que todas as faces estão a mesma distância da carga e fazendo o mesmo ângulo.
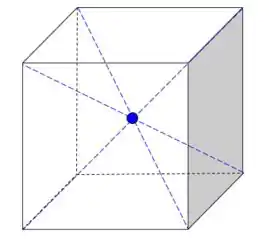
Sabendo que o fluxo pode ser escrito como
Como temos 6 faces, cada face recebe do fluxo.
Resposta
Exercícios de Livros Relacionados
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Uma linha de cargas com densidade linear uniforme λ está sobre o eixo x desde x = 0 até x = a . Mostre que a componente y do campo elétrico em um ponto do eixo y é dada por y = k λ y a y 2 + a 2 , y ≠