A constante solar, quantidade de energia solar que chega à Terra por unidade de tempo e área, acima da atmosfera e para um elemento de área perpendcular à direção dos raios solares, é de . Para um elemento de área cuja normal faz um ângulo com a direção dos raios solares, o fluxo de energia varia com . (a) Calcule a quantidade total de energia solar que chega à Terra por dia. Sugestão: Para um elemento de superfície , leve em conta a interpretação de como projeção sobre um plano (Capítulo 1, problema 8). (b) Sabe-se que da energia solar incidente sobre a água vão produzir evaporação. O calor latente de vaporização da água à temperatura ambiente (quantidade de calor necessária para vaporizá-la por unidade de massa) é . Sabendo que da superfície da Terra são cobertos por oceanos, calcule a profundidade da camada de água dos oceanos que seria evaporada por dia pela energia solar que chega à Terra.
Passo 1
Vamos começar fazendo um desenho da situação:
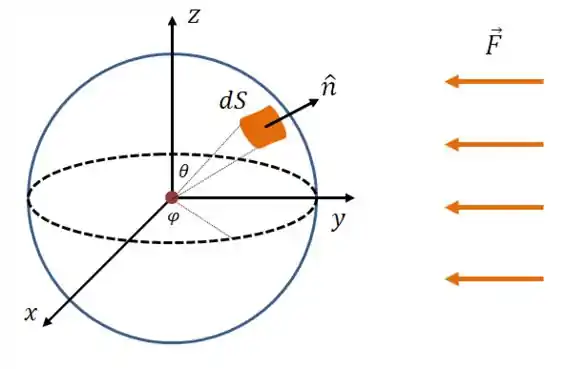
A potência que chega até uma pequena área é a seguinte:
Onde é a constante solar que foi dada no enunciado. Para encontrar a potência total só precisamos integrar essa equação ao longo da superfície:
Passo 2
Vamos calcular esse produto interno. Podemos escrever da seguinte forma:
Quando estamos em (e ), a situação é:
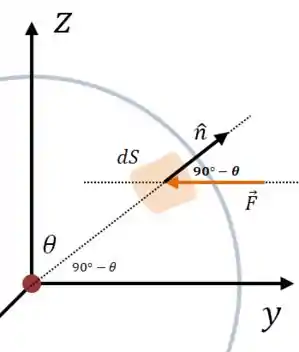
E então, como é um vetor unitário, o produto interno é:
Quando saímos do plano , só precisamos adicionar o para corrigir a diferença:
E a área em coordenadas esféricas segue a mesma fórmula de sempre:
Então nossa integral é:
O ângulo varia de até (indo do pólo norte ao pólo sul), e o ângulo também varia de até , já que só precisamos cobrir a metade do planeta que está iluminada pelo sol, então:
Agora podemos resolver a integral.
Passo 3
Vamos começar tirando as constantes da integral:
E podemos separar isso em duas integrais:
Vamos resolver essas duas integrais separadamente. Começando pela integral da esquerda:
E para a integral da direita:
Então:
Passo 4
Se essa é a potência recebida pela superfície da Terra, então ao longo de um dia, a energia total é:
Onde é a duração de um dia em segundos, então:
Substituindo o valor que foi dado no enunciado para e usando para o raio da Terra:
Passo 5
(b) O enunciado diz que aproximadamente dessa energia vão incidir sobre a água, e disso só vão produzir evaporação, então:
E se o calor latente de vaporização da água é calorias por grama, então a quantidade de água evaporada por dia é:
Mas precisamos converter esse calor latente para joules por grama (multiplicando cada caloria por ):
E já que a densidade da água é , isso corresponde ao seguinte volume de água:
Passo 6
Agora queremos saber qual a profundidade da camada de água que evapora.
Já que da superfície está coberta por água, então a área coberta é:
Então o volume ocupado por uma camada de água de altura é:
Portanto, para o volume de que nós calculamos:
Essa é a profundidade da camada evaporada a cada dia.
Resposta
(a) .
(b) .