Uma barra de secção transversal constante de de área tem de comprimento, dos quais de alumínio e de cobre. A extremidade de alumínio está em contato com um reservatório térmico a , e a de cobre com outro a . A condutividade térmica do alumínio é de e a do cobre é de . (a) Qual é a temperatura da barra na junção entre o alumínio e o cobre? (b) Se o reservatório térmico a é uma mistura de água com gelo fundente, qual é a massa de gelo que se derrete por hora? O calor latente de fusão do gelo é .
Passo 1
Vamos começar fazendo um desenho da situação:
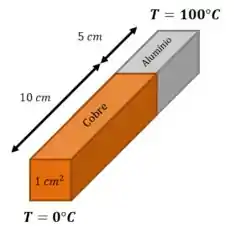
Vamos lembrar da fórmula para a taxa de transferência de calor:
Onde é a condutividade térmica do material, é a área das superfícies de contato, é a diferença de temperatura entre elas e é a distância entre elas.
Passo 2
(a) Nosso primeiro objetivo é encontrar a temperatura na junção entre cobre e alumínio, marcado com o plano azul na figura:

Para resolver isso, vamos igualar as taxas de transmissão de calor nas duas porções:
A área da superfície de contato é a mesma para os dois casos, então podemos cortar:
Agora vamos substituir com os valores numéricos que foram dados:
E então:
Passo 3
(b) Agora vamos imaginar o seguinte: se o reservatório de fosse feito de gelo, qual seria a massa derretida em um intervalo de uma hora.
Começamos calculando a taxa de transferência de calor naquela extremidade:
Temos que tomar muito cuidado com as unidades:
Passo 4
E então, como uma hora tem , a energia total transferida para o reservatório seria:
Agora vamos calcular a massa de gelo que pode ser derretida com essa energia. Sabendo que o calor latente de fusão do gelo é :
Resposta
(a) A temperatura na junção é .
(b) A massa de gelo derretida ao longo de uma hora é .