Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 27.Questões Conceituais - Ex. 2
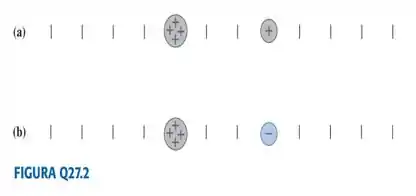
Copie a FIGURA Q27.2 em uma folha. Em cada item, desenhe um ponto ou vários pontos sobre a figura a fim de mostrar qualquer posição ou posições (que não sejam infinitamente distantes) onde .
Passo 1
Fala aí galerinha, blz??
Vamos para nossa segunda questão conceitual!
Bom! Pra resolver esse problema, precisamos saber duas coisas...
Uma, a fórmula do campo elétrico...
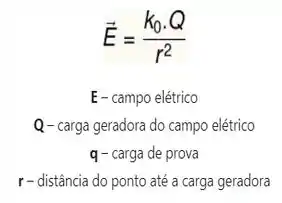
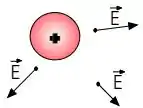
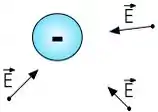
E dois, que o campo elétrico das cargas positivas sempre aponta para fora das cargas, na direção radial. Já o campo elétrico das cargas negativas aponta para dentro delas.
Passo 2
Pois muito bem! Como podemos ver na figura, nas letras (a) e (b), temos duas cargas separadas entre si... Em cada situação o módulo de uma carga aparenta ser quatro vezes maior que o da outra...
Assim, sabendo em como as linhas de campo elétrico se comportam, espera-se que a resposta da letra (a) esteja situada entre as duas cargas, ao passo que a resposta da letra (b) esteja situada perto de uma carga, mas longe da outra...
Mas calma que eu vou explicar matematicamente... Vamos considerar que a distância entre as duas barrinhas seja ...
(a) A resposta da primeira letra vai ser o seguinte...
Esse ponto azul aí da figura, vai ser onde ... E podemos explicar isso fazendo a configuração vetorial dos campos... Temos que...
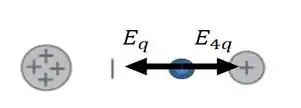
Somando assim, os dois campos já que eles se opõem...
Passo 3
(b) Já pra segunda letra, esse vai ser o ponto onde ...
Onde temos a seguinte distribuição vetorial...
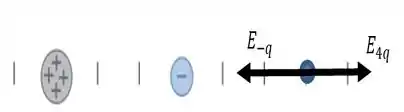
Assim, basta fazer a soma...
Pronto! Sucesso, gurizada!
Resposta
Ei, a resposta está no passo a passo :)