Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas - Ex. 80
80- Três cargas puntiformes são distribuídas ao longo do eixo ; uma carga no ponto , uma carga na origem e uma carga no ponto . Esse arranjo é chamado de quadrupolo elétrico
Determine o módulo, a direção e o sentido do campo elétrico nos pontos positivos sobre o eixo .
Use a série binomial para obter uma expressão aproximada para o campo elétrico válido para . Compare esse comportamento ao campo elétrico produzido por uma carga puntiforme e ao campo produzido por um dipolo elétrico.
Passo 1
A questão ficou esquisita, na real é uma carga em , outra carga em e uma carga na origem. Considerando que queremos saber o campo elétrico em um ponto no eixo qualquer nós temos o seguinte sistema.
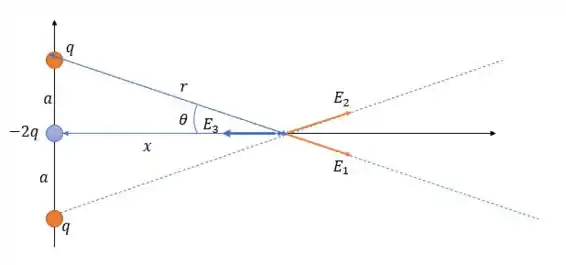
Onde o valor de será:
E o valor do campo elétrico é causada pela carga em e o valor de é pela carga em e o campo é causada pela carga em , e seu valores serão iguais a:
A parcela em do campo elétrico total será anulada pois os valores de são iguais para e (pois são os únicos vetores que tem parcela em ) e o valor total será em e será:
Ou seja:
Então:
Pois consegue-se notar que o campo é maior que a parcela em causada pelas partículas de carga . Então o campo elétrico resultante será da direita para a esquerda. Agora isolando dentro do parênteses nós teremos:
Sentido no eixo x
Passo 2
Nós podemos escrever o campo elétrico da seguinte forma:
Pela série binomial nós teremos que:
Só que como então podemos utilizar somente o primeiro termos de modo que teremos:
Se é muito grande então o campo elétrico tende a zero.