Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 20.1 - Ex. 60
Um cubo de cobre enegrecido com bordas de de comprimento é aquecido a uma temperatura de e, em seguida, é colocado em uma câmara de vácuo cujas paredes estão a uma temperatura de . Na câmara de vácuo, o cubo esfria radiativamente. (a) Mostre que a temperatura (absoluta) T do cubo segue a equação diferencial: onde é a capacidade térmica do cubo, é sua área de superfície, a emissividade e a temperatura da câmara de vácuo. (b) Usando o método de Euler (Seção 5.4 do Capítulo 5), resolva numericamente a equação diferencial para encontrar e faça um gráfico. Suponha que . Quanto tempo leva para o cubo esfriar a uma temperatura de ?
Passo 1
(a)Vamos relacionar a lei de Stefan-Boltzmann com a equação de taxa de calor para a variação de temperatura para obtermos a equação diferencial que descreve o resfriamento do cubo de cobre, a lei é:
E pela definição da capacidade térmica:
Passo 2
Igualamos as duas e isolamos
Passo 3
Para fazermos o gráfico da letra (b), precisaremos calcular o valor da capacidade térmica, para isso, basta utilizarmos a sua definição e reescrevê-la em termos da densidade e do volume:
Substituindo valores numéricos:
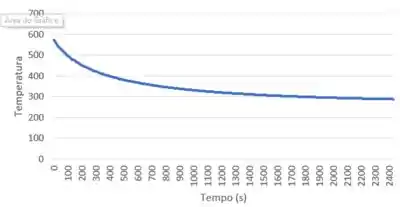
E então podemos fazer o gráfico:
Resposta
Ei, a resposta está no passo a passo :)