Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 22.Exercício - Ex. 6a
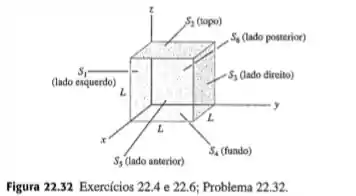
O cubo na Figura possui uma aresta . O campo elétrico é uniforme, paralelo ao plano , formando um ângulo de medido do eixo para o eixo , e possui módulo . Qual é o fluxo elétrico através de cada uma das seis faces do cubo , , e ? Qual é o fluxo elétrico total através de todas as faces do cubo?
Passo 1
Sabendo que o fluxo elétrico é dado por:
Temos que essa equação define o fluxo de um campo elétrico que passa perpendicularmente por uma área.
Então, o que se quer dizer é que devemos determinar, para cada uma das faces do cubo, um vetor normal a área das faces que define o sentido do fluxo. Logo:
No entanto, o campo elétrico não passa perpendicularmente pelas faces, tendo um leve desvio. Para ficar melhor, eis um esboço:
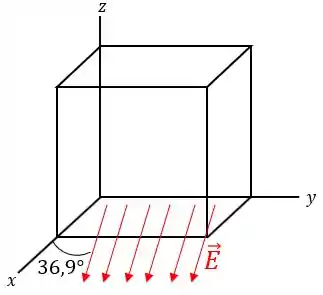
Para tanto, sabemos ainda que a área das faces é :
Passo 2
Dessa forma, vamos determinar todos os vetores direção de cada face.
O primeiro se encontra na face tal que o sentido está para o lado negativo do eixo e, portanto:
Seguindo a mesma ideia, as outras faces cujo vetor normal segue para valores positivos do seu respectivo eixo são e . Já as que seguem para valores negativos são e .
Com isso:
Passo 3
Agora, podemos encontrar o valor do fluxo em cada lado do cubo. Como o campo elétrico está paralelo ao plano , não possui componente , podemos concluir que os fluxos nas faces e são nulos.
Entretanto, para as outras partes: