Uma linha longa que possui densidade linear de carga uniforme corre paralelamente à superfície de uma placa de plástico plana e grande, a de distância, e que possui uma densidade superficial de carga uniforme de em um dos lados. Ache a localização de todos os pontos em que uma partícula não sofreria nenhuma força produzida por essa combinação de objetos carregados.
Passo 1
Fazendo um esboço da linha e da placa:
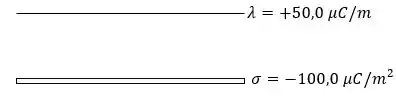
Como eles possuem sinais contrários de densidade, as regiões para que uma partícula não sofra ação de nenhuma força são aquelas em que os campos elétricos de ambas se anulam, ou seja, possuem mesma intensidade e sinais contrários.
Passo 2
Logo, o que queremos encontrar é:
Tal que, deixando em função das densidades, os campos elétricos serão dados pelas equações de uma linha infinita e de um plano infinito:
E, portanto, a distância será calculada por:
Logo, a partícula não sofreria nenhuma força em qualquer parte a da linha ou da placa nas partes externas.
Resposta
externamente