Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 31

31. Uma curva de auto-estrada de concreto, com 70   m de raio, é inclinada lateralmente em um ângulo de 15 ° . Qual é o máximo valor de velocidade com que um pneu de carro, feito de borracha, pode fazer esta curva sem derrapar?

Passo 1

Opa! Aqui vamos nós de novo!

Olha só! Esse é um clássico problema de relacionar força de atrito com movimento circular.

Sendo assim, vamos começar fazendo o diagrama de corpo livre para o nosso carro, que vai ter a seguinte cara da imagem abaixo...

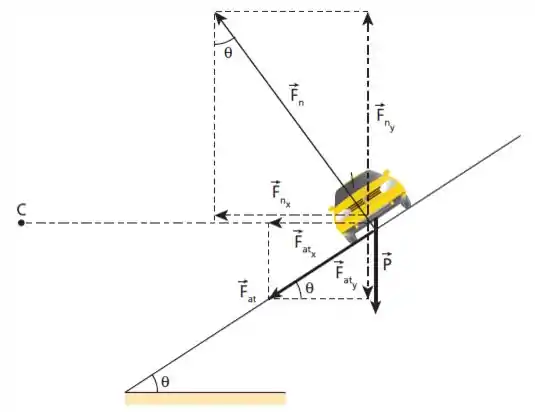
E também sabemos dos seguintes dados...

m = 1500   k g

r = 70   m

θ = 15 °

μ s = 1,0

Esse coeficiente de atrito, igual a 1,0 , advém do fato de que a questão nos diz que a pisa é de concreto! Esse é geralmente o valor do coeficiente de atrito para o concreto!

Passo 2

Feito essa parte introdutória, vamos ao que interessa.

Bora aplicar o somatório das forças na direção x , que é a direção radial, afinal essa é a direção onde está a resultante centrípeta, responsável pelo movimento circular.

∑ F x = m a r

F a t x + F n x = m v 2 R

F a t cos ⁡ θ + F n sen ⁡ θ = m v 2 R   ( 1 )

Depois, vamos aplicar o somatório das forças na direção y . Nessa direção, nosso garoto está em equilíbrio...

∑ F y = 0

F n y - F a t x - P = 0

F n cos ⁡ θ - F a t sen ⁡ θ - F G = 0   ( 2 )

Como a força de atrito F a t é o produto da força normal F n pelo coeficiente de atrito μ s ...

F a t = F n μ s

Então, substituindo em ( 1 ) ...

F a t cos ⁡ θ + F n sen ⁡ θ = m v 2 R

F n μ s cos ⁡ θ + F n sen ⁡ θ = m v 2 R

F n ( μ s cos ⁡ θ + sen ⁡ θ ) = m v 2 R

F n = m v 2 R ⋅ ( μ s cos ⁡ θ + sen ⁡ θ )   ( 3 )

E depois em ( 2 ) ...

F n cos ⁡ θ - F a t sen ⁡ θ - F G = 0

F n cos ⁡ θ - F n μ s sen ⁡ θ - F G = 0

F n cos ⁡ θ - F n μ s sen ⁡ θ = F G

F n cos ⁡ θ - F n μ s sen ⁡ θ = m g

F n cos ⁡ θ - μ s sen ⁡ θ = m g

F n = m g cos ⁡ θ - μ s sen ⁡ θ   ( 4 )

Obtivemos duas novas equações!

Passo 3

Igualando ( 3 ) e ( 4 ) ...

m v 2 R ⋅ ( μ s cos ⁡ θ + sen ⁡ θ ) = m g cos ⁡ θ - μ s sen ⁡ θ

v 2 R ⋅ ( μ s cos ⁡ θ + sen ⁡ θ ) = g cos ⁡ θ - μ s sen ⁡ θ

v 2 = g R ( μ s cos ⁡ θ + sen ⁡ θ ) cos ⁡ θ - μ s sen ⁡ θ

v = g R ( μ s cos ⁡ θ + sen ⁡ θ ) cos ⁡ θ - μ s sen ⁡ θ

Sabendo que θ = 15 ° e substituindo os outros valores correspondentes...

v = g R ( μ s cos ⁡ θ + sen ⁡ θ ) cos ⁡ θ - μ s sen ⁡ θ

v = ( 9,81   m / s ² ) ( 70   m ) ( 1,0 ⋅ cos ⁡ 15 ° + sen ⁡ 15 ° ) cos ⁡ 15 ° - 1,0 ⋅ sen ⁡ 15 °

v = 34,48   m / s

Essa é a máxima velocidade com que o carro pode fazer a curva!

Resposta

v = 34,48   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um carro fica sem gasolina e desce uma colina em ponto-morto. Ele prossegue assim atravessando o vale e começa a subida pelo outro lado. Para o momento em que o carro passa exatamente pelo fundo do va
Tarzan balança-se na floresta pendurado em um cipó. No ponto mais baixo do balanço, o valor da tensão no cipó é maior, menor ou igual à intensidade da força gravitacional sobre Tarzan? Explique.
Em cada um dos Problemas de 53 a 54 lhe é fornecida uma equação (ou equações) a ser usada na resolução. Em cada caso, você deve:a. Redigir um problema realista para o qual a equação se aplique. Verifi
Uma bola de 60g é presa à extremidade de um barbante de 50c m de comprimento e girada em um círculo vertical. O centro do círculo, como mostra a FIGURA P 8.48 , encontra-se 150 c m acima do piso. A bo
Em cada um dos Problemas de 53 a 54 lhe é fornecida uma equação (ou equações) a ser usada na resolução. Em cada caso, você deve:a. Redigir um problema realista para o qual a equação se aplique. Verifi