Exercícios de Movimento Circular Uniforme - Lista de Exercícios Resolvida
Questão 1
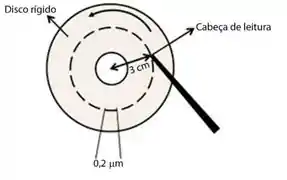
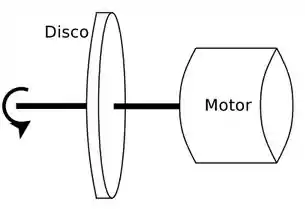
Considere um computador que armazena informações em um disco rígido que gira a uma frequência de 120 Hz. Cada unidade de informação ocupa um comprimento físico de 0,2μm na direção do movimento de rotação do disco. Quantas informações magnéticas passam, por segundo, pela cabeça de leitura, se ela estiver posicionada a 3 cm do centro de seu eixo, como mostra o esquema simplificado apresentado abaixo? (Considere π ≈ 3.)
a)
b)
c)
d)
Ver solução completaQuestão 2
Anemômetros são instrumentos usados para medir a velocidade do vento. A sua construção mais conhecida é a proposta por Robinson em 1846, que consiste em um rotor com quatro conchas hemisféricas presas por hastes, conforme figura abaixo. Em um anemômetro de Robinson ideal, a velocidade do vento é dada pela velocidade linear das conchas. Um anemômetro em que a distância entre as conchas e o centro de rotação é r=25 cm, em um dia cuja velocidade do vento é v=18 km/h, teria uma frequência de rotação aproximadamente de
Se necessário, considere π = 3.

a) 3 rpm.
b) 200 rpm.
c) 720rpm.
d) 1200 rpm.
Ver solução completaQuestão 3
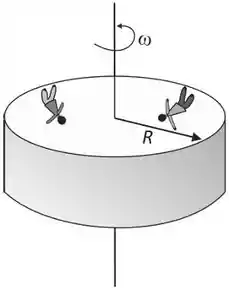
Uma estação espacial foi projetada com formato cilíndrico, de raio R igual a 100 m, como ilustra a figura abaixo. Para simular o efeito gravitacional e permitir que as pessoas caminhem na parte interna da casca cilíndrica, a estação gira em torno de seu eixo, com velocidade angular constante ω. As pessoas terão sensação de peso, como se estivessem na Terra, se a velocidade ω for de, aproximadamente,
a) 0,1 rad/s
b) 0,3 rad/s
c) 1 rad/s
d) 3 rad/s
e) 10 rad/s
Note e adote:
A aceleração gravitacional na superfície da Terra é g = 10 m/s2
Ver solução completaQuestão 4
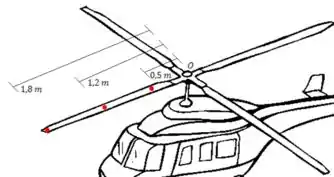
Um helicóptero que está se preparando para decolar, liga suas hélices. Nesse momento a hélice possui velocidade constante, realizando uma volta completa em . Determine a velocidade angular das pás do helicóptero e o deslocamento em cada ponto marcado em vermelho, mostrado no desenho abaixo, após 4 segundos.
Questão 5
Uma bolsa a do centro e uma carteira a do centro descrevem um movimento circular uniforme no piso de um carrossel. Elas estão na mesma linha radial. Em um certo instante, a aceleração da bolsa é . Qual é a aceleração da carteira nesse instante, em termos dos vetores unitários.
Ver solução completaQuestão 6
Uma partícula descreve um movimento circular uniforme de raio em um plano horizontal, em um sistema de coordenadas onde a origem se encontra no centro da circunferência. Qual destas afirmações é falsa:
- A velocidade média depois de um período completo é nula
- A velocidade escalar média depois de um período completo é igual a
- O produto escalar entre o vetor velocidade e o vetor posição da partícula é sempre nulo.
- O produto escalar entre o vetor velocidade e o vetor aceleração da partícula é sempre nulo.
- O produto escalar entre o vetor aceleração e o vetor posição da partícula é sempre nulo.
Questão 7
Em uma parque de diversões uma mulher passeia em uma roda-gigante com 15 m de raio, completando 5 voltas em torno do eixo horizontal a cada minuto. Quais são:
- O período do movimento?
- O módulo da aceleração centrípeta no ponto mais alto?
- O sentido da aceleração centrípeta no ponto mais alto?
- O módulo da aceleração centrípeta no ponto mais baixo?
- O sentido da aceleração centrípeta no ponto mais baixo?
Questão 8
Um corredor mantém em uma pista circular uma velocidade constante de 2m/s e completa uma volta em 80 s. Determine a frequência de giro do corredor e o tamanho da pista circular.
a) 0,00150 Hz e 180 m
b) 0,0125 Hz e 170 m
c) 0,0125 Hz e 160 m
d) 0,0325 Hz e 180 m
e) 0,0525 Hz e 160 m
Ver solução completaQuestão 9
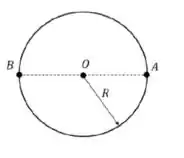
1) Um carro descreve um movimento circular uniforma com velocidade de módulo constante em uma pista circular de raio , ilustrada na figura abaixo. Qual o módulo da aceleração média , no deslocamento do ponto ao ponto ?
a)
b)
c)
d)
e)
Ver solução completaQuestão 10
7) Um planeta cujo dia tem duração de horas possui uma lua (satélite natural). A distância entre os centros dos dois astros é km e o satélite completa uma volta em órbita circular com centro do planeta a cada 5 dias. Os módulos das velocidades de translação do centro do satélite em torno do planeta em e sua aceleração em são, respectivamente:
(a) e
(b) e
(c) e
(d) e
(e) e
Ver solução completaQuestão 11
3) Uma partícula de massa está presa a um fio ideal de comprimento cuja outra extremidade está fixada ao teto. Largada do repouso, a partícula faz um ângulo com a vertical como indica a figura. O módulo da velocidade da partícula no momento que chega ao ponto mais baixo é:
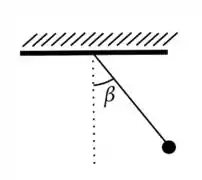
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 12
Uma partícula descreve um movimento circular uniforme de raio em um plano horizontal, em um sistema de coordenadas onde a origem se encontra no centro da circunferência. Qual destas afirmações é falsa:
- A velocidade média depois de um período completo é nula
- A velocidade escalar média depois de um período completo é igual a
- O produto escalar entre o vetor velocidade e o vetor posição da partícula é sempre nulo.
- O produto escalar entre o vetor velocidade e o vetor aceleração da partícula é sempre nulo.
- O produto escalar entre o vetor aceleração e o vetor posição da partícula é sempre nulo.
Questão 13
O vetor aceleração em um movimento circular uniforme:
- É variável em módulo e varia de direção
- É nulo pois o movimento é uniforme, com velocidade constante
- É constante em módulo e varia em direção
- Nenhuma das alternativas é correta ou duas ou mais alternativas são corretas
- É variável em módulo e não varia de direção
- É constante em módulo e não varia de direção
Questão 14
(Capítulo 9.1 – Exercício 35) Uma roda varre em ao ser levada ao repouso com aceleração angular constante. Determine a rapidez angular inicial da roda ao começar a ser freada.
Ver solução completaQuestão 15
Uma criança em um carrossel executa um movimento circular uniforme tal que no instante inicial sua velocidade em relação a um referencial cuja origem está no centro do carrossel. Se após sua velocidade é a aceleração centrípeta da criança vale:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 16
Q - Uma partícula desloca-se no sentido anti-horário, sobre um círculo de raio com vetor velocidade que varia com o tempo segundo a equação (no SI). Sabe-se que em sua posição angular é . A posição angular da partícula no instante em que ela inverte o sentido do movimento, em radianos, é:
Ver solução completaQuestão 17
Uma bola de boliche de raio é lançada com velocidade sobre uma superfície plana horizontal, sem movimento rotacional. O coeficiente de atrito cinético entre a bola de boliche e a superfície é . Enquanto desliza, por causa do atrito com a superfície, a bola inicia um movimento rotacional, até que passa a descrever um movimento de rolamento, rolando sem deslizar.
- Calcule a aceleração do centro de massa e a aceleração angular da bola enquanto ela desliza sobre a superfície.
- Determine o instante de tempo no qual a bola passa a rolar sem deslizar.
Questão 18
Uma pequena bola de massa está presa em um fio, apoiada em uma mesa horizontal e sem atrito. A bola executa um movimento circular uniforme com velocidade angular inicial e raio . O fio passa por um furo na mesa. Uma pessoa então puxa o fio lentamente até que o raio da trajetória final torne-se .
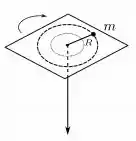
Seja o módulo do momento angular inicial da bola e o módulo do seu momento angular final. Do mesmo modo, é a energia cinética inicial e a energia cinética final. Podemos dizer que
Questão 19
Uma partícula pode ter sua velocidade vetorial variável, se o módulo da velocidade for constante.
Ver solução completaQuestão 20
Um anel de raio gira com velocidade angular constante relativa à terra em torno de um eixo fixo perpendicular ao plano do anel e que passa pelo seu centro. Uma formiga se move sobre o anel no sentido em que ele gira. A velocidade da formiga relativa ao anel é de módulo constante . Em um dado instante, a formiga passa por um ponto P marcado no anel. No instante em que ela volta ao ponto P pela primeira vez, verifica-se que o anel deu 3 giros completos. Qual a relação entre e ?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 21
Uma roda-gigante com 10,0 de raio faz uma revolução a cada 24 . Ao chegar à parte mais alta do percurso, praticamente a um diâmetro de distância do solo, um passageiro deixa cair uma pedra. A que distância do ponto do solo diretamente abaixo do centro da roda-gigante cai a pedra? Utilize se necessário =3.
a) 0
b) 1,0 m
c) 5,0 m
d) 6,1 m
e) 10,0 m
Ver solução completaQuestão 22
2. Um projétil de massa é lançado com uma velocidade horizontalmente e na direção norte a partir de uma posição de colatitude . Determine a direção e a magnitude da força de Coriolis em termos de , , e da velocidade angular da Terra . Como a força de Coriolis se compara ao peso do projétil se e ?
Ver solução completaQuestão 23
No dia 15/02/2013, um meteorito atingiu a cidade de Chelyabinsk, na Rússia, deixando em torno de 950 pessoas feridas, a maioria sem gravidade. Diversas imagens registradas por câmeras de monitoramento foram divulgadas pelas agências internacionais de notícias. Imediatamente cientistas da Agência Espacial Europeia utilizaram algumas dessas imagens em busca da localização de fragmentos do meteorito, descrevendo equações utilizadas no ajuste para localizar sua posição em função do tempo através de uma modelagem simples de movimento de projétil. Suponha que a equação de ajuste para a posição do meteorito (), determinada a partir de uma imagem adquirida por uma câmera de segurança de uma residência (), haja sido, em função do tempo, dada por:
Em um sistema de coordenadas onde os eixos e definem o plano horizontal e o eixo vertical.
a) Determine os vetores velocidade e aceleração do meteorito determinados pela câmera de segurança da residência, respectivamente descritos por , .
Suponha agora que esta mesma câmera de segurança () haja podido registar, na mesma imagem, a passagem de um automóvel () pela rua durante a queda do meteorito, fornecendo uma equação de ajuste para a posição do automóvel dada por:
b) Considerando que o tempo de queda do meteorito até a colisão com a Terra foi de aproximadamente 5 segundos, determine o deslocamento escalar total realizado pelo automóvel durante este tempo. (atenção: este ítem independe do )
c) Sabendo que o automóvel também possuía uma câmera e pôde registrar o movimento do meteorito, determine os vetores posição e velocidade do meteorito medidos por esta câmera, respectivamente descritos por , .
O próximo ítem é independente dos três anteriores:
d) Considere agora que, instantes antes da queda do meteorito, o automóvel esteja parado aguardando para entrar em uma rotatória de 20 metros de raio. Ele observa uma motocicleta já contornando a curva e estima que, quando esta moto está a um ângulo de 60° à sua direita (veja figura), ela possui uma velocidade escalar de . Determine o vetor aceleração da motocicleta neste instante, escrevendo-o explicitamente em termos dos vetores unitários do sistema de referência apresentado.
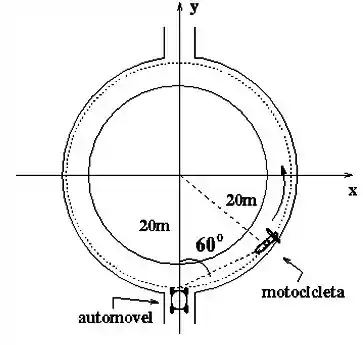
Questão 24
A Terra tem a forma aproximado de uma esfera de raio . O valor aproximado da circunferência da Terra em é:
A.
B.
C.
D.
E.
Ver solução completaQuestão 26
Sabemos que o comprimento de um círculo é dado por (onde, é o comprimento, e é o raio da circunferência). Em cada período, o movimento circular uniforme executa (um) comprimento circular. A frequência é o inverso do período. Com essas informações você está preparado para resolver o exercício proposto.
Duas polias de raios e estão ligadas entre si por uma correia. Sendo e sabendo-se que a polia de raio efetua , a frequência da polia de raio , em , é:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 27
Um carro de corrida efetua uma trajetória em um circuito circular de diâmetro igual a com módulo de velocidade constante igual a . O período do movimento é:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 28
Até o século XV, a Música era considerada uma ciência Matemática, que juntamente com a Aritmética, Geometria e a Astronomia compunham o Quadrivium.
A relação entre a Matemática e a Música é bastante antiga, mas se evidencia cientificamente com os experimentos de Pitágoras (séc VI a.e.c.), que conseguiu organizar os sons em uma escala musical por meio de seus experimentos com um monocórdio, partindo das divisões de uma corda.
A amplitude da onda equivale à propriedade do som de ser forte ou fraco, ou seja, a Intensidade.
A frequência equivale à altura da nota. Sendo assim, se executássemos 261 pulsos em um segundo obteríamos a nota Dó.
O período é o tempo compreendido entre estados iguais de vibração.
Fonte: http://matematicaemusica.pbworks.com/w/page/20503556/Sen%C3%B3ide ¿ Acesso: 9:35 h do dia
26/08/2011
Sabemos que o comprimento de um círculo é dado por e que em cada período o movimento circular uniforme executa (um) comprimento circular.
A frequência é o inverso do período.
Com essas informações você está preparado para resolver o exercício abaixo.
(FUND. CARLOS CHAGAS) Duas polias de raios e estão ligadas entre si por uma correia. Sendo e sabendo-se que a polia de raio efetua , a frequência da polia de raio , em , é:
Fonte:http://www.coladaweb.com/exercicios-resolvidos/exercicios-resolvidos-de-fisica/movimentos-circulares.
Acesso: 16:39 h do dia 25/08/2011.
(a) 60.
(b) 120.
(c) 15.
(d) 7,5.
(e) 30.
Ver solução completaQuestão 29
Um ponto material descreve uma circunferência horizontal com velocidade constante. O raio da circunferência vale e o ponto em questão completa uma volta a cada . Podemos afirmar que a velocidade angular para o ponto material mencionado vale, em :
Obs: Lembrem-se que e que
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 30
Roda mundo, roda gigante
Roda moinho, roda pião
O tempo rodou num instante
Nas voltas do meu coração...
Trecho da música Roda Viva de Chico Buarque.
Nesta música, Chico Buarque, trata do turbilhão que novas vidas se transformam. Neste trecho, especificamente, temos destacados movimentos de rotação. Sabemos que todo movimento de rotação está associado à aceleração centrípeta, que tem como fórmula: onde é a velocidade e é o raio.
O movimento de rotação tem uma ligação com a grandeza física:
(a) Impulso.
(b) Potência.
(c). Energia Cinética
(d) Energia Potencial
(e). Momento Linear
Ver solução completaQuestão 31
Uma partícula de massa executa um MCU no sentido anti-horário com raio e período . O centro da sua trajetória coincide com a origem do sistema de coordenadas.
No instante , o vetor posição da partícula em metros é . No instante , a força centrípeta (em newtons) agindo na partícula é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 32
Um corpo de massa percorre, com velocidade angular constante , em sentido
anti-horário, uma trajetória circular de raio , cujo centro dista da origem do sistema de coordenadas , como mostra a figura.
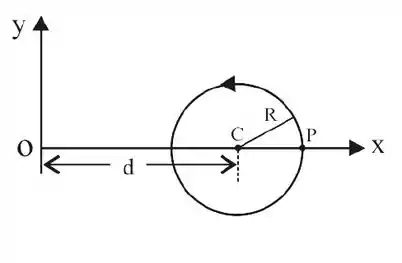
Sabendo que o corpo está passando pelo ponto no instante , a equação que descreve sua posição em relação à origem do sistema de coordenadas, em função do tempo , é dada por:
Os símbolos e representam vetores unitários, perpendiculares entre si, nas direções e sentidos dos eixos x e y, respectivamente.
Ver solução completaQuestão 33
Em um motor elétrico típico, a curva de torque é aproximadamente constante na faixa de rotações de trabalho do motor. Suponha que o eixo deste motor está conectado à uma roda de massa , em formato de cilindro. Sabendo que o torque do motor é dado por , obtenha a aceleração angular e a velocidade angular em função do tempo .
Questão 34
10) Um disco começa a rotacionar com aceleração angular constante em torno de um eixo que passa pelo seu centro. Em certo instante , ele gira a 10 rps (rotações por segundo). Após mais 62,5 voltas, no instante , sua velocidade angular atinge 15 rps. Calcule o intervalo de tempo em segundos.
- 5,0
- 31,4
- 62,8
- 3,14
Questão 35
Na análise do movimento circular uniforme, uma das grandezas mais importantes é o período do movimento. Podemos afirmar que o período é:
(a) O intervalo de tempo mínimo para que um fenômeno cíclico se repita.
(b) A aceleração de um fenômeno cíclico.
(c) A quantidade de vezes que um fenômeno cíclico deve se repetir para que o mesmo consiga seguir uma trajetória.
(d) A frequência de ocorrência de um fenômeno cíclico.
(e) O número de ciclos que ocorre na unidade do segundo.
Ver solução completaQuestão 36
Um automóvel que se move a possui pneus com de diâmetro.
Qual é a velocidade angular dos pneus em relação aos respectivos eixos?
Se o carro é freado com aceleração constante e as rodas descrevem voltas completas (sem deslizamento), qual é o módulo da aceleração angular das rodas?
Que distância o carro percorre durante a frenagem?
Ver solução completaQuestão 39
Uma partícula se move em uma trajetória circular horizontal no plano , com velocidade escalar constante. No instante , a partícula possui velocidade e aceleração no sentido positivo de . No instante , a partícula possui velocidade e aceleração no sentido positivo de . Considere a diferença é menor que um período de rotação.
Encontre o raio do círculo e o módulo da aceleração centrípeta.
Ver solução completaQuestão 40
Um disco de raio gira em torno do seu centro com período de rotação igual a , como ilustrado na figura. Considere que a figura representa o disco em .
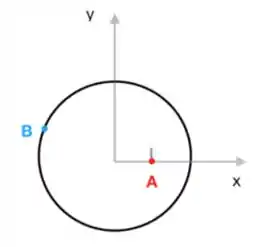
a) Calcule a aceleração centrípeta do ponto A.
b) Forneça a posição do ponto A em .
c) Determine a velocidade escalar e angular do ponto B em .
d) Numa mesma figura, faça o gráfico de dos pontos A e B no intervalo de tempo .
Ver solução completaQuestão 41
Uma moeda de massa está sobre um disco rígido a uma distância do centro do disco. Existe atrito entre a moeda e o disco e o coeficiente estático é . Num tempo , o disco começa a girar com uma aceleração angular constante de magnitude em torno do seu eixo central. A magnitude da aceleração da gravidade é . Expresse suas respostas em termos de , , , , e , se necessário.
- Qual é a magnitude máxima da força de atrito estático?
- Como a força de atrito estático varia em função do tempo?
- Qual a magnitude da velocidade angular que a moeda começa a deslizar do disco?
Questão 42
Para ligar um cortador de grama, você deve puxar uma cordinha que está enrolada ao longo do perímetro de um volante. Depois de você puxar a corda por , o volante está girando a revoluções por segundo quando a cordinha se desprende. Esta tentativa de ligar o cortador não funciona, no entanto, e o volante acaba por parar após do desprendimento da cordinha. Suponha aceleração constante, tanto durante a puxada da cordinha quanto durante o freamento do volante. (a) Determine a aceleração angular média durante os em que a cordinha está sendo puxada e durante os do fretamento do volante. (b) Qual é a maior rapidez angular atingida pelo volante? (c) Determine a razão entre o número de voltas realizadas na primeira etapa e o número de voltas realizadas na segunda etapa.
Ver solução completaQuestão 43
(Capítulo 9.1 – Exercício 37) A fita em um videocassete VHS padrão tem um comprimento total de , o suficiente para operar durante . Quando no início, o carretel cheio tem um raio externo de e um raio interno de . Em algum momento da operação, os dois carretéis têm a mesma rapidez angular. Calcule esta rapidez angular em radianos por segundo e em revoluções por minutos. Dica: Entre os dois carretéis, a fita corre com rapidez constante.

Questão 44
- Considere uma partícula que realiza um movimento circular com rapidez constante. Sobre este movimento, podemos afirmar que
- Existe somente uma força atuando sobre a partícula.
- O movimento não é acelerado.
- A aceleração da partícula é constante.
- A magnitude da aceleração da partícula é constante.
- A direção da aceleração da partícula é tangente ao círculo.
Ver solução completaQuestão 45
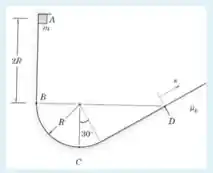
Um pequeno bloco de massa é liberado do repouso na posição deslizando ao longo da pista no plano vertical. Sabendo que a pista é lisa de até e rugosa em diante,
- Faça um diagrama de forças para o bloco nos pontos e .
- Quais são as forças normais exercidas pela pista sobre o bloco quando este passa pelas posições e ?
- Determine as velocidades do bloco nos pontos B e D
- Qual é a distância s percorrida pelo bloco ao longo da inclinação após passar pelo ponto D, até ele parar.
Use R=10m, 0.2, g=9,8
Questão 46
(Cap 4 – Ex 74) Um avião leve atinge uma velocidade do ar de . O piloto pretende chegar a um ponto ao norte, mas descobre que deve direcionar o avião a leste do norte para atingir o destino. O avião chega em . Quais eram
(a) o módulo e
(b) a orientação da velocidade do vento?
Ver solução completaQuestão 47
(Cap 4 – Ex 65) Em , a aceleração de uma partícula em movimento circular no sentido anti-horário é . A partícula se move com velocidade escalar constante. Em , a aceleração é . Qual é o raio da trajetória da partícula se a diferença é menor que um período de rotação?
Ver solução completaQuestão 48
Um objeto está se movendo em uma trajetória circular com metros de raio a uma velocidade escalar constante de . O tempo necessário para uma revolução é:
A.
B.
C. .
D. .
E.
Ver solução completaQuestão 49
Em um movimento circular uniforme onde os vetores posição, velocidade e aceleração da partícula valem e , respectivamente, (considere a origem do sistema de referência no centro do círculo) marque a alternativa correta para o resultado das seguintes equações:
, e /()
A. , respectivamente;
B. , respectivamente;
C. , respectivamente;
D. . , respectivamente;
E. , respectivamente;
Ver solução completaQuestão 50
Um estudante observa uma partícula que se movimenta em MCU e relata que a mesma executa voltas a cada segundos. Analisando esses dados, podemos afirmar que a conclusão do estudante quanto ao período (em ) e a frequência do movimento (em ) foi que eles valem, respectivamente:
(a) e
(b) e
(c) e
(d) e
(e) e
Ver solução completaQuestão 51
(Cap 4 – Ex 61) Um carrossel de um parque de diversões gira em torno de um eixo vertical com velocidade angular constante. Um homem em pé na borda do carrossel tem uma velocidade escalar constante de e uma aceleração centrípeta de módulo O vetor posição indica a posição do homem em relação ao eixo do carrossel.
(a) Qual é o módulo de ? Qual é o sentido de quando aponta
(b) para leste e
(c) para o sul?
Ver solução completaQuestão 52
8. Um carro percorre uma curva de raio não inclinada. O coeficiente de atrito estático entre os pneus e o solo é de . Qual é a máxima velocidade com que o carro poderá fazer a curva sem derrapar.
Questão 53
4. Uma bola de está suspensa por dois fios ideiais presos na haste horizontal que gira em torno de um eixo vertical como mostra a figura.
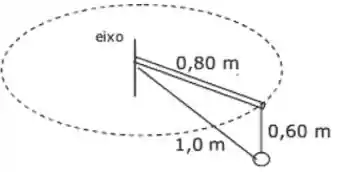
A bola descreve um trajetória circular horizontal de raio com rapidez de . O comprimento do fio vertical é de e do fio inclinado é de . Qual a tensão aproximada do fio vertical?
Questão 54
9. Em , um objeto inicia um movimento circular de raio igual a a partir do repouso com aceleração tangencial constante de . Em que instante o módulo da sua aceleração tangencial é igual ao módulo da sua aceleração centrípeta?
Questão 55
- Considere uma partícula que realiza um movimento circular com rapidez constante. Sobre este movimento, podemos afirmar que
- Existe somente uma força atuando sobre a partícula.
- O movimento não é acelerado.
- A aceleração da partícula é constante.
- A magnitude da aceleração da partícula é constante.
- A direção da aceleração da partícula é tangente ao círculo.
Ver solução completaQuestão 56
4. Uma bola de está suspensa por dois fios ideiais presos na haste horizontal que gira em torno de um eixo vertical como mostra a figura.
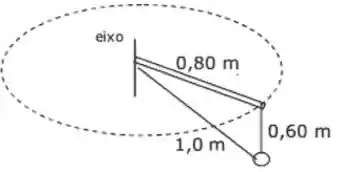
A bola descreve um trajetória circular horizontal de raio com rapidez de . O comprimento do fio vertical é de e do fio inclinado é de . Qual a tensão aproximada do fio vertical?
Questão 57
3. Ao passar pelo ponto mais baixo de um loop circular de uma montanha russa de raio , a força normal aplicada no passageiro de massa igual a pelo banco sobre o qual ele está sentado é igual a . Quanto vale a velocidade do passageiro nesse ponto?
Questão 58
8. Um carro percorre uma curva de raio não inclinada. O coeficiente de atrito estático entre os pneus e o solo é de . Qual é a máxima velocidade com que o carro poderá fazer a curva sem derrapar.
Questão 59
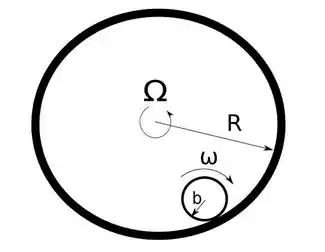
Uma bola de raio e massa está rolando sem deslizar sobre um anel de raio . A velocidade angular da bola é . Suponha que o anel está rodando com uma velocidade angular . Qual é a velocidade linear do centro de massa da bola em relação ao centro do anel? Escreva sua resposta com as variáveis do exercício.
Questão 60
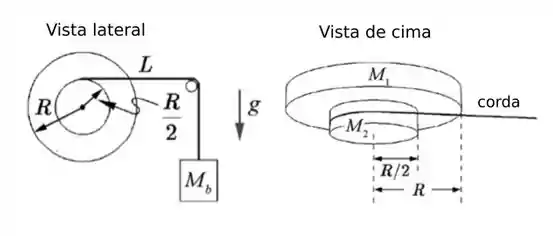
Considere uma roda fixa que consiste de um disco cilíndrico uniforme de raio e massa e um segundo disco cilíndrico uniforme de raio e massa que está encaixado concentricamente ao primeiro disco. A roda gira livre de atrito em torno do eixo central. Uma corda é enrolada em torno do disco menor. A ponta livre é atada a um bloco de massa de tal forma que os dois discos girem enquanto o bloco desce. A aceleração da gravidade tem magnitude . O bloco é solto do repouso. Qual o tempo para o bloco cair de uma distância ? Dê sua resposta em função das variáveis do problema.
Questão 61
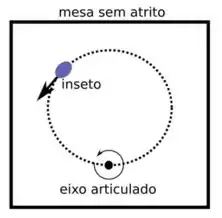
Um anel de raio e massa está deitado sobre uma mesa sem atrito. Ele é articulado por um eixo na sua borda. Um inseto de massa anda sobre o anel com uma velocidade constante relativo ao anel, e começando no eixo articulado, quando o anel está em repouso. Assuma o eixo para fora da página.
- Qual é a velocidade angular do anel quando o inseto está na metade da volta?
- Qual é a velocidade angular do anel quando o inseto está de volta ao eixo articulado?
Questão 62
Uma haste rígida e uniforme de comprimento e massa está deitada sobre uma mesa sem atrito e é articulada por um eixo no ponto em uma de suas extremidades. Um objeto pontual de massa está movendo para direita com velocidade . Ele colide e gruda na haste a uma distância do eixo articulado. Um segundo objeto pontual também de massa movendo para a esquerda também atinge e gruda na haste no mesmo instante que o primeiro objeto, mas a uma distância . O momento de inércia da hasta para um eixo que passa pelo seu centro de massa e paralelo ao eixo articulado é . Depois da colisão o sistema rotacional sobre o eixo articulado está com velocidade angular .
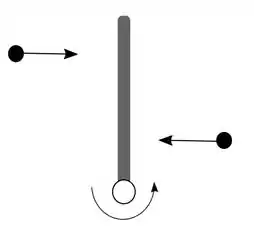
- Qual é a velocidade angular ?
- Qual é a razão entre a energia cinética inicial e final do sistema ?
Questão 63
Num movimento circular uniforme de raio igual a metros, uma partícula descreve um deslocamento angular de radianos em segundos. Qual a distância percorrida (em metros) pela partícula e a frequência do movimento em (Hertz)?
A. e
B. e
C. e
D. e
E. e
Ver solução completaQuestão 64
Um modelo de rotor de helicóptero tem 4 lâminas, cada uma com de comprimento, do eixo central à ponta. A frequência de rotação do rotor dentro do túnel de vento é de .
(b) Determine a aceleração radial da ponta da lâmina, expresse como múltiplo da aceleração da gravidade, .
Ver solução completaQuestão 65
A centrífuga de um laboratório na terra faz n rpm e produz aceleração de na sua extremidade mais externa.
(a) Calcule a aceleração (em ) num ponto na metade do caminho em relação à extremidade?
Ver solução completaQuestão 66
A centrífuga de um laboratório na terra faz rpm e produz aceleração de na sua extremidade mais externa.
(b) Essa centrífuga agora é utilizada como uma cápsula espacial no planeta Mercúrio, onde é da gravidade local terrestre. A quantos rpm (em termos de ) deve estar para produzir na extremidade exterior?
Ver solução completaQuestão 67
Um modelo de rotor de helicóptero tem 4 lâminas, cada uma com de comprimento, do eixo central à ponta. A frequência de rotação do rotor dentro do túnel de vento é de .
(a) Qual a velocidade linear da ponta das lâminas, em m/s?
Ver solução completaQuestão 68
A corda da figura tem comprimento e a distância até o pino fixo é de . A bola é liberada, a partir do repouso, com a corda na posição horizontal, descrevendo a trajetória indicada pela linha tracejada como mostra a figura. Qual é a velocidade da bola:
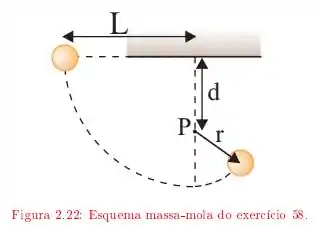
Mostre que para que a bola faça uma volta completa em torno do pino (Sugestão: A bola ainda deve estar se movendo quando chegar ao ponto mais alto da trajetória).
Ver solução completaQuestão 69
A corda da figura tem comprimento e a distância até o pino fixo é de . A bola é liberada, a partir do repouso, com a corda na posição horizontal, descrevendo a trajetória indicada pela linha tracejada como mostra a figura. Qual é a velocidade da bola:
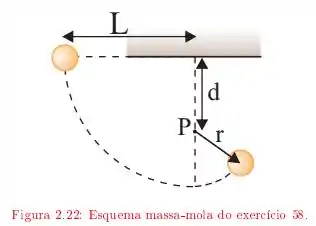
quanto está passando pelo ponto mais baixo da trajetória?
Ver solução completaQuestão 70
A corda da figura tem comprimento e a distância até o pino fixo é de . A bola é liberada, a partir do repouso, com a corda na posição horizontal, descrevendo a trajetória indicada pela linha tracejada como mostra a figura. Qual é a velocidade da bola:
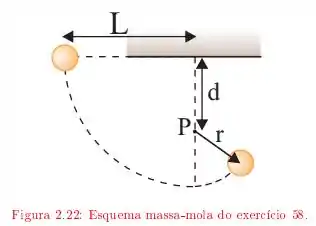
quando chega ao ponto mais alto da trajetória depois que a corda toca o pino?
Ver solução completaQuestão 71
Uma conta de massa enfiada em um aro circular de raio situado em um plano vertical, está presa por uma mola de constante de mola ao ponto , localizado no topo do aro. Na posição relaxada da mola, ela está localizada em , o qual é o ponto mais baixo do aro. Se soltarmos a conta, a partir do repouso, do ponto , que faz um ângulo de com , como indicado na figura , com que velocidade ela atinge o ponto ?
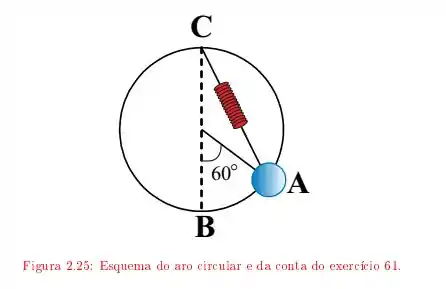
Questão 72
Um projétil de massa se move para direita com velocidade conforme figura ao lado. O projétil atinge e adere à extremidade de uma barra de massa , comprimento , que pode rotacionar em torno de um eixo que passa pelo centro. (a) Encontre a velocidade angular do sistema logo após a colisão. (b) Determine a perda de energia mecânica devido à colisão.
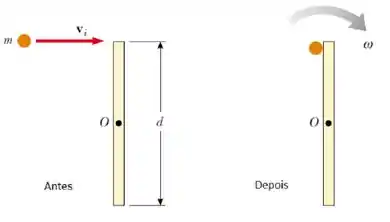
Questão 73
Duas caixas e com massas e , respectivamente, estão presas por cordas a uma haste que gira com velocidade angular de magnitude . A caixa está a uma distância da haste e a caixa está a uma distância . Ignore as massas das cordas e o efeito da gravidade. Expresse suas respostas nas constantes descritas.
- Calcule , a tensão na corda que conecta a caixa na .
- Calcule , a tensão na corda que conecta a caixa na haste.
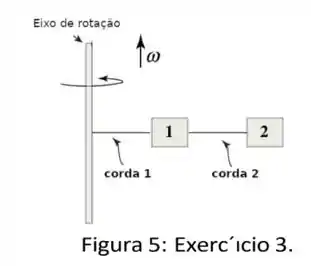
Questão 74
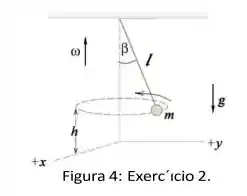
Uma bolinha de massa é suspensa por um cordão de comprimento , O cordão faz um ângulo com a vertical. A bolinha orbita em círculos com velocidade angular desconhecida, O plano orbital da bolinha está a uma altura do chão. Seja a constante da aceleração da gravidade, Ignore a resistência do ar.
- Descubra a velocidade angular . Use as constantes explicitadas no problema.
- A bolinha se solda do cordão e atinge o chão a uma distância horizontal de onde se soltou. Qual é essa distância ?
Questão 75
No final de uma corda de massa e comprimento está presa uma haste que gira com magnitude da velocidade angular . Na outra extremidade, está presa um objeto pontual de massa . Descubra a tensão na corda em função da distância da haste.
Assuma que o raio da haste é muito menor que o comprimento da corda. Ignore os efeitos da gravidade e expresse sua resposta em termo das variáveis e constantes apresentadas no problema.
Questão 76
Uma partícula executa um movimento circular uniforme (MCU) no plano , com centro na origem e sentido anti-horário. Em certo instante o seu vetor velocidade (em m/s) vale . No instante , o vetor posição da partícula é , onde R é o raio do MCU.
Sabendo que o período do MCU é , qual é a sua aceleração centrípeta (em ) no instante ?
Questão 77
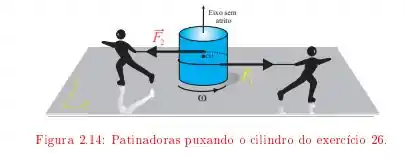
Um disco uniforme de e raio está sobre uma superfície de gelo lisa. Duas patinadoras gêmeas enrolam cordas em torno do disco, num mesmo sentido. Depois cada qual puxa a sua corda e se afasta do disco, exercendo sobre ele forças constantes e durante .
Quais são a aceleração angular e a velocidade angular em função do tempo?
Questão 78
Em uma centrífuga girando a 1000 rpm (revoluções por minuto), uma partícula se encontra a 0,200 m do eixo de rotação. Calcule a razão r= /g entre as magnitudes da aceleração centrípeta desta partícula e da aceleração da gravidade g.
(A)
(B)
(C )
(D)
(E)
Ver solução completaQuestão 79
Um disco, um anel e uma esfera maciça de mesmo raio e massa descem rolando num plano inclinado, sem deslizar. É correto afirmar que:
- a esfera chega primeiro na base do plano inclinado;
- o anel chega primeiro na base do plano inclinado;
- chegaram juntos na base do plano inclinado;
- o disco chega antes que a esfera na base do plano inclinado
- o disco chega primeiro na base do plano inclinado;
Questão 80
A figura a seguir mostra um objeto uniforme que rola sem deslizar sobre um plano inclinado. O objeto possui massa , raio e momento de inércia ao redor do eixo de rotação. Sabe-se que quando o objeto é liberado do repouso a partir de uma certa altura , ele é lançado horizontalmente ao chegar à base do plano inclinado, tocando o solo a uma distância horizontal do ponto de lançamento.
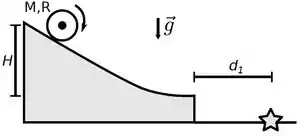
Na iminência do lançamento horizontal o centro de massa do cilindro possui uma velocidade . Sabendo que o , qual é o período de rotação do cilindro em torno de seu centro de massa?
Dado: considere
Questão 81
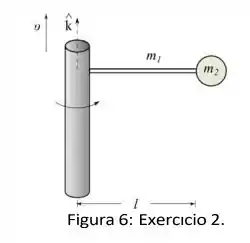
Um sistema composto por duas pequenas esferas de mesma massa e dois fios ideais de mesmo comprimento descreve um movimento circular uniforme conforme mostrado na figura abaixo.

Considerando o Movimento Circular Uniforme descrito pelo sistema, qual a única correta das afirmativas abaixo?
(a) A tensão nos dois fios é a mesma.
(b) O módulo da velocidade linear das duas esferas é o mesmo.
(c) As duas esferas possuem uma componente tangencial da aceleração diferente de zero.
(d) A componente radial da aceleração das duas esferas é a mesma.
(e) A velocidade angular das duas esferas é a mesma.
Ver solução completaQuestão 82
Dois satélites estão orbitando a Terra em altitudes diferentes. Assuma que as órbitas são circulares e os satélites têm a mesma massa. Qual satélite possui maior velocidade linear em torno da Terra? Qual satélite tem um maior período ?
Ver solução completaQuestão 83
A respeito do movimento circular uniforme, podemos afirmar que o mesmo se caracteriza por:
(a) módulo da aceleração centrípeta nula e módulo da velocidade constante.
(b) é composto por aceleração que independe do raio da trajetória curvilínea.
(c) é composto somente por aceleração vetorial.
(d) aceleração centrípeta constante e velocidade nula.
(e) módulo da aceleração centrípeta constante e módulo da velocidade constante.
Ver solução completaQuestão 84
Um disco homogêneo, de massa e raio , move-se no plano horizontal em rotação pura ao redor do eixo vertical fixo , que tangencia a borda do disco e é perpendicular ao plano . O vetor momento angular do disco, em relação à origem do sistema de coordenadas, é dado por , em unidades do SI. Se em , o disco está girando com velocidade angular , podemos afirmar que o seu raio , em centímetros, é:
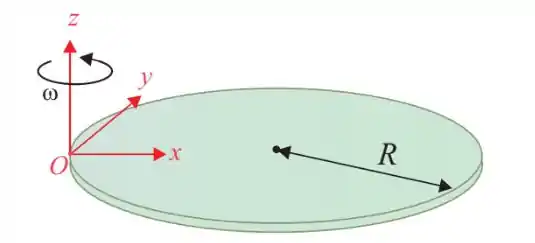
O momento de inércia de um disco de massa e raio em relação ao eixo de rotação que passa pelo seu centro de massa e é perpendicular ao plano é
a)
b)
c)
d)
e)
Ver solução completa